Основные логические понятия. Логические уровни.
Входной сигнал по своей природе может быть чисто дискретным, например импульсы в детекторе частиц или «биты» информации, поступающие от ключа, клавиатуры или ЭВМ. В подобных случаях естественно и удобно использовать цифровую электронику, т. е. схемы, которые имеют дело с информацией, представленной в виде «единиц» или «нулей».
Для того чтобы непрерывную (аналоговую) информацию можно было обрабатывать на ЭВМ или хранить в виде чисел, ее необходимо преобразовать в цифровую форму и наоборот (с помощью цифро-аналоговых ЦАП и аналого-цифровых АЦП-преобразователей). Характерным примером служит ситуация, в которой микропроцессор или ЭВМ воспринимает сигналы от экспериментальной или промышленной установки, на основе полученных данных управляет параметрами эксперимента и хранит полученные результаты для последующего использования в процессе эксперимента.
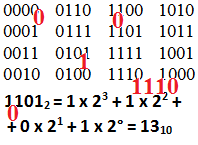
Другим интересным примером, который демонстрирует возможности цифровых методов, является передача аналоговых сигналов без искажений, связанных с воздействием помех. Например, звуковые и видеосигналы, передаваемые по кабелю или с помощью радиоволн, воспринимают «шум», который потом нельзя отделить от полезного сигнала. Если же передаваемый сигнал преобразовать в ряд чисел, определяющих его амплитуду в последовательные моменты времени. Затем эти числа передавать в виде цифровых сигналов. В таком случае аналоговый сигнал, восстановленный на приемной стороне (с помощью ЦАП), не будет содержать ошибок, Конечно, если уровень шума в канале связи не настолько высок, чтобы помешать правильному распознаванию «единиц» и «нулей».
Этот метод, известный под названием импульснокодовой модуляции (ИКМ), особенно эффективен в том случае, когда сигнал должен проходить через ряд ретрансляторов. Например, при межконтинентальной телефонной связи. Восстановление цифрового сигнала в каждом пункте ретрансляции гарантирует помехоустойчивую передачу. Космические зонды с помощью ИКМ передают на землю данные и изображения. Цифровая звукозапись в вашем доме размещается на цифровых носителях информации, которые хранят стереомузыкальные произведения в виде 16 разрядов каждые 23 мкс, порядка 6 млрд бит информации на все.
Возможности цифровой аппаратуры настолько велики, что задачи, предназначенные, казалось бы, исключительно для аналоговых методов, гораздо лучше зачастую решаются цифровым путем. Например, в аналоговом измерителе температуры можно установить микропроцессор и память, в результате этого повысится точность измерений за счет компенсации нелинейности прибора. Подобные применения микропроцессоров стали обычным делом.
Высокий и низкий уровни
Под цифровой электроникой подразумевается, как правило, только два состояния, например транзистор может быть либо закрыт, либо насыщен. В качестве параметра обычно выбирают не ток, а напряжение, уровень которого может быть ВЫСОКИМ или НИЗКИМ.
Эти два состояния могут представлять различные «биты» (binary digits-двоичные разряды) информации, например, следующим образом:
один бит числа — ключ замкнут или разомкнут, присутствует или отсутствует сигнал, уровень аналогового сигнала выше или ниже заданного предела, некоторое событие произошло или не произошло, требуется или не требуется выполнять некоторые действия и т.п.
Состояния ВЫСОКОГО и НИЗКОГО уровней определяют некоторым заданным образом «истинные» и «ложные» значения в булевой алгебре. Если в какой-либо точке схемы истинное значение определяет ВЫСОКИЙ уровень, то говорят, что эта сигнальная линия использует «положительную логику» и наоборот. Пример «отрицательной логики» показан на рисунке 1.
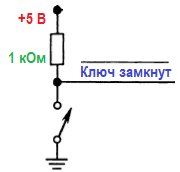
Когда состояние КЛЮЧ ЗАМКНУТ истинно, выход имеет НИЗКИЙ уровень. Выходной сигнал, таким образом, соответствует «отрицательной логике» (более правильным было бы название «нулевая логика», поскольку отрицательное напряжение в схеме отсутствует) и может быть обозначен, как показано на рисунке 1.
Черта над символом означает операцию НЕ, т. е. данная линия имеет ВЫСОКИЙ уровень, когда ключ не замкнут. Наличие или отсутствие черты отрицания над обозначением говорит о том, какой уровень (ВЫСОКИЙ или НИЗКИЙ) будет иметь данный провод, когда заданное условие (КЛЮЧ ЗАМКНУТ) истинно.
Цифровая схема «знает», что за сигнал она представляет по тому, откуда поступает этот сигнал, так же как в аналоговой схеме выход какого-либо операционного усилителя «представляет» определенную величину. Цифровые схемы, однако, обладают дополнительной гибкостью. Иногда одни и те же сигнальные линии используются для передачи различных видов информации и для посылки ее в разных направлениях в различные моменты времени. Для того чтобы выполнить это «мультиплексирование», необходимо посылать дополнительную информацию (адресные биты или биты состояния).
Понятия 1 и 0 используются в булевой алгебре для обозначения утверждений ИСТИНА и ЛОЖЬ соответственно. В том же значении они иногда используются и в электронике, но, к сожалению, здесь они применяются также и в другом смысле, а именно:
1 означает высокий уровень (символ В), а 0 — НИЗКИЙ уровень (символ Н).
Диапазон напряжений высокого и низкого уровней.
Значения напряжений, соответствующих ВЫСОКИМ и НИЗКИМ уровням, могут колебаться в некотором диапазоне. Например, для высокоскоростной КМОП логики входные напряжения от уровня земли до 1,5 В представляются как НИЗКИЙ уровень, а напряжения в пределах 1,5 В от напряжения питания 4-5 В — как ВЫСОКИЙ уровень. Типичные напряжения НИЗКОГО и ВЫСОКОГО состояний составляют десятую долю В выше 0 и ниже 5 В соответственно (остаточное напряжение одного МОП-транзистора).
Такие широкие диапазоны выбраны для того, чтобы изготовитель микросхем имел в своем распоряжении определенный допуск, в пределах которого параметры схемы могли бы колебаться за счет изменения температуры, нагрузки, напряжения питания, а также под воздействием шумов.
Схема, получив сигнал, определяет, каков его уровень (ВЫСОКИЙ или НИЗКИЙ), и действует соответствующим образом. Если помеха не превращает 1 в 0 или наоборот, то все прекрасно и любые помехи отсеиваются на каждой ступени, поскольку на выходе схемы восстанавливаются «чистые» значения 1 или 0. Цифровая электроника в этом смысле не подвержена влиянию помех и является идеальной.
Термин помехоустойчивость используется здесь для обозначения максимального уровня помехи, которая, будучи добавлена к логическому сигналу при самых неблагоприятных условиях, не будет еще приводить к ошибочной работе схемы. Например, для элементов ТТЛ помехоустойчивость составляет 0,4 В, так как любой сигнал ниже 0,8 В интерпретируется ими как НИЗКИЙ уровень, а любой сигнал выше 2,0 В-как ВЫСОКИЙ, в то время как уровни выходных сигналов составляют в самом неблагоприятном случае 4-0,4 и 4-2,4 В соответственно. В действительности помехоустойчивость этих схем значительно выше приведенной величины, поскольку типичные значения ВЫСОКОГО и НИЗКОГО напряжений составляют 4-0,2 и 3,4 В, а входной порог принятия решения равен ~ 1,3 В.
Однако необходимо помнить, что хорошая схема рассчитана на самый неблагоприятный случай. Не следует также забывать о том, что различные семейства логических элементов обладают различной помехоустойчивостью. Элементы КМОП имеют по сравнению с ТТЛ более высокую помехоустойчивость, а быстродействующие элементы ЭСЛ (эми́ттерно-свя́занной ло́гики) — более низкую. Конечно, восприимчивость к шуму цифровых систем зависит также от амплитуды шума, которая в свою очередь зависит от таких факторов, как параметры выходной ступени индуктивности проводников земли, существования длинных линий «шин», скорости нарастания на выходе во время логического перехода (когда из-за емкостной нагрузки возникают переходные токи, вызывающие выбросы напряжения линии земли).
Диаграмма на рисунке 2 показывает диапазоны напряжений, которые соответствуют двум логическим состояниям (ВЫСОКИЙ и НИЗКИЙ) для самых популярных семейств цифровой логики. Для каждого логического семейства необходимо определить допустимые значения как входных, так и выходных напряжений, соответствующих состояниям ВЫСОКИЙ и НИЗКИЙ.
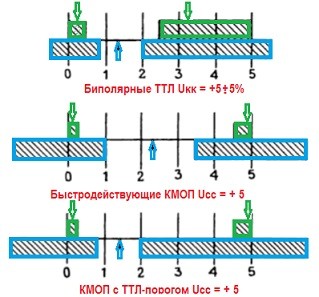
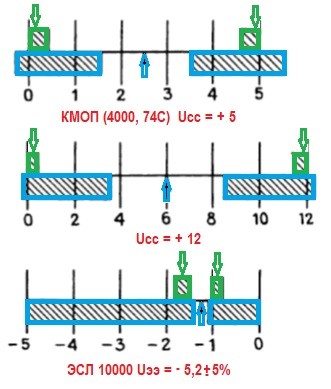
Закрашенная площадь выше линии
показывает допустимый диапазон выходных напряжений, при котором гарантируются логические состояния НИЗКИЙ и ВЫСОКИЙ без ошибок. Две стрелки сверху 
, указывают типовые выходные значения (НИЗКИЙ и ВЫСОКИЙ), встречающиеся на практике.
Закрашенная площадь ниже линии
показывает диапазон входных напряжений, гарантирующий представление как НИЗКИЙ или ВЫСОКИЙ. Стрелка внизу
указывает типовое напряжение логического переключения, т. е. линию, разделяющую уровни НИЗКИЙ и ВЫСОКИЙ. Во всех случаях логическое состояние ВЫСОКИЙ более положительно, чем логическое НИЗКИЙ.
Значения «минимальный», «типовой» и «максимальный» в электронных спецификациях требуют нескольких слов для пояснения. Наиболее часто, изготовитель гарантирует, что компоненты будут попадать в диапазон минимум-максимум с наибольшей вероятностью к «типовому». Для используемых типовых спецификаций при проектировании схем это означает, что схемы должны работать надежно внутри диапазона, заданного минимумом и максимумом. В частности, хорошо спроектированная схема должна функционировать при всех возможных комбинациях минимальных и максимальных значений (даже на самый плохой случай).
Числовые коды
В большинстве случаев рассмотренные выше условия, которые могут быть представлены цифровыми уровнями, просты и наглядны. Более сложный и интересный вопрос заключается в том, как с помощью цифровых уровней представить часть числа.
Десятичное (с основанием 10) число представляет собой строчку из цифр. При этом подразумевается, что они должны быть умножены на последовательные степени числа 10 для образования индивидуальных произведений, а затем вместе сложены.
Например,
137,06 = 1 х 10² + 3 х 10¹ + 7 х 10° + 0 х 10-1 + 6 х 10-2.
Для записи числа требуется десять символов (от 0 до 9), а степень числа 10, на которую должна быть умножена цифра, определяется ее положением по отношению к десятичной запятой.
Если мы хотим представить число с помощью только двух символов (0 и 1), то такая система счисления будет называться двоичной или системой с основанием 2. В этом случае каждая 1 или 0 будет умножаться на последовательные степени числа 2.
Например,
11012 = 1 х 23 + 1 х 22 + 0 х 21 + 1 х 2° = 1310
Отдельные «единицы» и «нули» в записи, представляющей двоичное число, называются «битами» (от слов binary digits-двоичный разряд). Индекс (записываемый всегда по основанию 10) указывает, какая используется система счисления. Он часто бывает нужным для того, чтобы избежать путаницы, так как все символы выглядят одинаково.
Только что описанный метод преобразует число из двоичной формы в десятичную. Для того чтобы произвести обратное преобразование, десятичное число нужно последовательно делить на 2, каждый раз записывая остаток.
Для преобразования числа 
в двоичное нужно произвести следующие операции:
13/2 = 6, остаток 1;
6/2 = 3, остаток 0;
3/2 = 1, остаток 1;
1/2 = 0, остаток 1;
это дает 
Заметим, что ответ образуется, начиная с младшего значащего разряда (МЗР).
Шестнадцатеричное представление чисел.
Для описания систем только с двумя состояниями естественно применять двоичные числа. Однако это не единственный способ. Поскольку двоичные числа имеют большую длину, для их записи используется шестнадцатеричное (с основанием 16) представление. Для записи двоичного числа в шестнадцатеричном коде его разбивают на группы по 4 бит, каждая из которых может принимать значения от 0 до 15. Поскольку для обозначения каждой шестнадцатеричной позиции мы хотим использовать один символ, величины 10-15 будем обозначать буквами латинского алфавита от А до F:
7071О = 10110000112 = (10 110000112) = 2С316.
Шестнадцатеричное представление лучшим образом соответствует байтовой (1 байт = 8 бит) структуре ЭВМ, которая чаще всего реализуется в виде 16- или 32-разрядных машинных «слов». При этом каждое слово состоит из 2 или 4 байтов. Буквенно-цифровые знаки (буквы, цифры или символы) представляются в виде одного байта. Таким образом, каждый байт в шестнадцатеричной системе состоит из двух шестнадцатеричных цифр, 16-разрядное машинное слово из 4-х шестнадцатеричных цифр и т. д.
Например, в широко используемом коде ASCII:
— малое «а» в ASCII-представлении — 01100001 (61 в шестнадцатеричном коде, который записывается как 61н),
— «b» есть 62н и т. д.
Как другой пример, размещение памяти в компьютере с памятью 64Кb (65536 байт) может определяться 2-байтным адресом, поскольку 
наинизший адрес есть 0000н, наивысший-FFFFн. Вторая половина памяти начинается с 8000н, а четвертая четверть памяти — с С000н.
Можно случайно встретить «восьмеричную» запись (основание 8), к сожалению, в ранних ЭВМ были приняты 12- и 32-разрядные слова, которые использовали 6-разрядное представление буквенно-цифровых знаков. Поскольку 6-разрядные знаки было логично представлять в восьмеричном коде, внедрилась эта система счисления.
Двоично-десятичный код
Другим методом представления чисел является двоичное кодирование каждой десятичной цифры, записываемой в виде группы из 4 двоичных разрядов. Например,
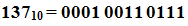
(двоично-десятичный код).
Заметим, что двоично-десятичное представление числа не эквивалентно двоичному, которое в данном случае будет иметь вид:
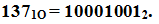
Можно считать, что разряды двоично-десятичного кода, начиная с правого, выражают числа 1, 2, 4, 8, 10, 20, 40, 80, 100, 200, 400, 800 и т.д. Очевидно, что двоично-десятичное кодирование с точки зрения использования двоичных разрядов не экономично, поскольку каждая группа из 4 бит способна представлять числа от 0 до 15, но используется для записи числа, не превышающего 9.
Двоично-десятичное кодирование очень удобно в тех случаях, когда требуется воспроизвести число в десятичной форме, так как в этом случае каждый двоично-десятичный символ нужно лишь преобразовать в соответствующее десятичное число, а затем вывести его на индикацию.
Для выполнения этой функции существуют специальные интегральные микросхемы. В одном небольшом корпусе с простой топологией они содержат дешифратор двоично-десятичного кода, формирователи сигналов, буферный регистр и индикатор. На вход такой схемы нужно лишь подать логические уровни двоично-десятичного символа, после этого на ней высвечивается соответствующая цифра.
По этой причине двоично-десятичное кодирование используется обычно при вводе и выводе цифровой информации. К сожалению, преобразование между двоично-десятичным и чисто двоичным кодом сложно, так как каждая десятичная цифра зависит от состояния почти всех двоичных разрядов и наоборот. Тем не менее двоичная арифметика настолько эффективна, что в большинстве ЭВМ вся входная информация преобразуется в двоичную форму, а обратное преобразование производится лишь при ее выводе.
Числа со знаком
Прямой (знаковеличинный) код.
Рано или поздно возникнет необходимость представлять отрицательные числа в двоичном коде. В первую очередь это потребуется в устройствах, которые выполняют вычислительные операции. Самое простое-отвести один разряд (скажем, старший) под знак числа, а остальные использовать для представления его величины. Этот способ называется знаковеличинным или прямым кодом и соответствует обычной записи числа со знаком (таблица 1).
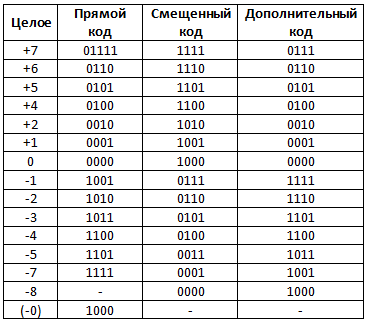
Он используется при выводе чисел на индикацию, а также в некоторых аналого-цифровых преобразователях (АЦП). Вообще же это не лучшая форма представления чисел со знаком, особенно при выполнении вычислений, так как в данном случае операции вычитания и сложения выполняются по-разному (т. е. сложение «не работает» для чисел со знаком). Кроме того, здесь могут присутствовать нули двух типов (+0 и -0), поэтому при выборе нужного из них следует быть очень внимательным.
Смещенный код.
Смещенный код является вторым методом представления числа со знаком. Чтобы получить смещенный код какого-либо числа, нужно к этому числу, представленному в прямом коде, прибавить половину наибольшего возможного числа (таблица 1). Последовательность всех чисел благодаря этой операции, начиная с наибольшего отрицательного числа и кончая наибольшим положительным числом, представляет простую двоичную прогрессию и может быть сформирована с помощью двоичных счетчиков. Информацию о знаке здесь также несет старший разряд, но нуль становится однозначным. Смещенный код используется в АЦП и ЦАП (преобразователях), однако он еще неудобен для выполнения вычислений.
Дополнительный код.
При выполнении операций над целыми числами чаще используется представление чисел в форме дополнения до двух, или, иначе, в дополнительном коде. В такой системе положительные числа записываются просто как двоичные без знака, а отрицательные выражаются таким числом, которое, будучи добавлено к положительному числу той же величины, даст в результате нуль. Чтобы получить отрицательное число, нужно для каждого бита положительного числа сформировать дополнение до 1, или обратный код (т. е. вместо каждого 0 записать 1 и наоборот), и затем к полученному результату прибавить 1 (это даст дополнительный код).
Из таблицы 1 видно, что числа в дополнительном коде отличаются от чисел в смещенном коде инверсным значением старшего значащего разряда (СЗР). Точно так же, как и при других формах представления, СЗР несет информацию о знаке. Здесь имеется только один нуль, который удобно представляется нулевыми состояниями всех разрядов (при очистке счетчика или регистра в них заносится нулевое значение).
Арифметика в дополнительном коде.
Арифметические операции в дополнительном коде выполняются довольно просто. Чтобы получить сумму двух чисел, достаточно сложить соответствующие разряды (с учетом переноса), например
5 + (-2): 0101 (+5)
________1110( -2)
0011(+3)
Чтобы вычесть В из А, нужно взять дополнительный код числа В и прибавить его к числу А (т. е. прибавить отрицательное число):
2 — 5:0010(+2)
1011 (-5)
1101(-3)
(+5 = 0101: обратный код-1010, дополнительный код-1011)
Умножение в дополнительном коде выполняется также непосредственно.
Дополнительный код благодаря естественности вычислений в нем повсеместно используется в ЭВМ для выполнения арифметических операций над целыми числами. Следует отметить, что числа с «плавающей запятой» обычно используются в знаковеличинной форме, называемой знак-порядок-мантисса.
Код Грея
Код, рассматриваемый ниже, используется в механических шифраторах угла поворота вала, а также в других устройствах. Он носит название кода Грея и обладает тем свойством, что при переходе от любого его состояния к следующему изменяется лишь один разряд (бит), что позволяет предотвратить ошибки, поскольку в данном случае при переходе между двумя закодированными значениями все разряды никак не могут измениться одновременно.
Если бы использовался чисто двоичный код, то при переходе, например, от 7 к 8 на входе можно было бы получить число 15. Для формирования состояний кода Грея существует простое правило:
начинать нужно с нулевого состояния, а затем для получения каждого следующего нужно выбрать самый младший разряд, изменение которого приводит к образованию нового состояния, и взять его инверсное значение.
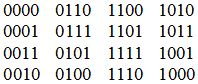
Коды Грея могут содержать любое число разрядов. Они применяются при «параллельном кодировании» — методе быстродействующего аналого-цифрового преобразования.
