Радиаторы для мощных транзисторов, отвод тепла, расчеты
Часто необходимо, использовать мощные транзисторы или другие сильноточные устройства, такие, как микросхемы преобразователей напряжения, стабилизаторы, симисторы или силовые выпрямители, рассеивающие мощности во много ватт. Все мощные устройства выпускаются в корпусах, обеспечивающих тепловой контакт между их металлической поверхностью и внешним радиатором. Во многих случаях металлическая поверхность устройства связана электрически с одним из выводов (например, у мощного транзистора она всегда связана с коллектором).

В принципе задача теплоотвода – удержать переходы транзисторов или других устройств. При этом температура, не должна превышать указанную для них максимальную рабочую температуру. Для кремниевых транзисторов в металлических корпусах максимальная температура переходов обычно равна 200 °C, а для транзисторов в пластмассовых корпусах равна 150 °C.
Зная температурные параметры, проектировать теплоотвод просто. Зная мощность, которую прибор будет рассеивать в данной схеме, подсчитываем температуру переходов с учетом теплопроводности транзистора, радиатора и максимальной рабочей температуры окружающей транзистор среды. Затем выбираем такой радиатор, чтобы температура переходов была намного ниже указанной изготовителем максимальной. Здесь разумно перестраховаться, так как при температурах, близких к максимальной, транзистор быстро выходит из строя.
Тепловое сопротивление
При расчете радиатора используют тепловое сопротивление Q, которое равняется отношению величины перепада температур в градусах к передаваемой мощности.
Q = (Т2 — Т1)/Р,
где Q – тепловое сопротивление на участке тепловой цепи, К/Вт
T2 – температура начала участка, К;
Т1 – температура конца участка, К;
Р – тепловой поток, протекающий через участок цепи, Вт
Если теплопередача происходит только путем теплопроводности, то тепловое сопротивление величина постоянная, не зависящая от температуры, а зависящая только от устройства теплового контакта. Для последовательного ряда тепловых контактов общее температурное сопротивление равно сумме тепловых сопротивлений отдельных соединений.
Для транзистора, смонтированного на радиаторе, общее тепловое сопротивление передаче тепла от кристалла на внешнюю среду равно сумме тепловых сопротивлений кристалл‑корпус Qпк, соединения корпус‑радиатор Qкр и перехода радиатор‑среда Qрс. Таким образом, температура кристалла будет равна:
Τкр = Τс + (Q пк + Q кр + Q рс) P
где Ρ – рассеиваемая мощность, Вт;
Τс — температура окружающей среды.
Рассмотрим пример. Допустим, у нас есть схема источника питания с внешним проходным транзистором. На транзисторе максимум рассеиваемой мощности 20 Вт при нестабилизированном входном напряжении +15 В (10 В падения напряжения, 2 А). Предположим, что эта схема должна работать при окружающей температуре 50 °C. Это не так уж невероятно для компактно расположенного электронного оборудования. Постараемся удержать температуру кристаллов ниже 150 °C, т. е. намного ниже, чем указанные изготовителем 200 °C.
Тепловое сопротивление от кристалла к корпусу указывается в технической литературе на транзистор как «Junction−to−Case» (RθJC). Предположим, что оно равно 1,5 °C/Вт. Специальная прокладка между корпусом транзистора, обеспечивающая электрическую изоляцию и тепловой контакт, имеет тепловое сопротивление от корпуса к радиатору порядка 0,3 °C/Вт. И наконец, радиатор.
Предположим, у нас имеется радиатор с тепловым сопротивлением на границе с внешней средой порядка 2,3 °C/Вт.
Таким образом общее тепловое сопротивление между кристаллом и внешней средой будет равно 1,5+0,3+2,3 = 4,1 °C/Вт. При рассеиваемой мощности 20 Вт температура перехода будет на 4,1х20 = 84 °C выше температуры окружающей среды, т. е. будет равна 84°C+50°C = 134°C. 50 °C — максимальная внешняя температура для данного случая.
Итак, такой выбранный радиатор будет пригоден, а если необходимо сэкономить пространство, то можно выбрать и несколько меньший.
Варианты подбора радиатора
Поскольку тепловое сопротивление радиатора далеко не всегда указывается, придется определять его самостоятельно. Тепловое сопротивление перехода радиатор среда Qрс можно посчитать по приблизительной формуле:
Qрс =51*k/S,
где Qрс – тепловое сопротивление радиатора в °C/Вт,
S – площадь радиатора (в данном случае — площадь детали) в см2,
k – коэффициент, учитывающий тип вентиляции (для естественной вентиляции принимают k = 33, для принудительной вентиляции k = 11).
Площадь радиатора вычисляется как сумма площадей всех его ребер, площади основания между ребрами и двойной площади сечения.
Так для простейшего радиатора 14х14х6 мм площадь поверхности в см2 равна:
S = (1,4*0,6*2+12*1,4*0,5) + (1,4*1,4-7*0,05*1,4) + (1,4*0,1+7*0,05*0,5) = 10,08+1,47+0,315 = 11,865 см2
Таким образом, тепловое сопротивление такого радиатора без принудительной вентиляции приблизительно равно
Qрс =51*33/11,865 = 141,8 °C/Вт

Давайте, для сравнения попробуем рассчитать, приблизительное тепловое сопротивление радиатора размером 47х35х17 мм для транзистора типа ТО-220.
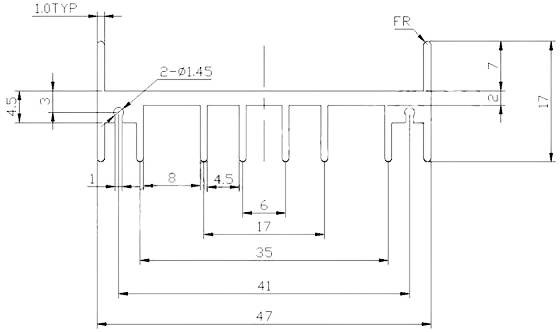
Складываем все площади в см:
Ребра
Sр = 0,7*3,5*2 + 1,7*3,5*2 + (1,7-0,7-0,45)*4*3,5 + (1,7-0,7-0,2)*10*3,5 + (0,1*10*3,5) = 4,9 + 11,9 +7,7 + 28 + 3,5 = 56 см2
Площадь поверхности между ребрами радиатора
Sмр = 0,8*2*3,5 + 0,45*3*3,5 + (4,7-3,5-0,1*2-0,1)*2*3,5 = 5,6 + 4,725 + 6,3 = 16,625 см2
Площадь поперечного сечения (складываем двойную площадь)
Sпс = 0,2*4,7 + 0,7*2*0,1 +0,9*8*0,1 = 0,94 + 0,14 +0,72 = 1,8 см2
Площадь задней поверхности между боковыми ребрами
Sзп = (4,7-0,1*2)*3,5 = 15,75 см2
От площади задней поверхности нужно отнять площадь соприкосновения с транзистором, но пока можно пренебречь. Складываем все площади:
Sобщ = 56 + 16,625 + 1,8*2 + 15,75 ≈ 92 см2
Находим тепловое сопротивление:
Qрс =51*33/92 = 18,3 °C/Вт
Т.е. на таком радиаторе при разнице температур радиатор-окружающая среда в 70°C можно рассеять почти 4 Вт мощности без принудительной вентиляции.
На практике принято также считать, что у ребристого радиатор с естественным охлаждением площадью15 кв.см рассеиваемая мощность 1 Вт (с улучшенной вентиляцией — 10 кв.см на 1 Вт, с принудительной вентиляцией — 4 кв.см на 1 Вт).
Для оценки тепловой мощности радиатора можно использовать следующую зависимость:
P= λ × (Tр—Tокр.ср )× S; [ Вт ]
где:
Tр — средняя температура поверхности радиатора, Tокр.ср — температура окружающей среды;
S — полная площадь теплоотдающей поверхности радиатора, м2.
λ — эффективный коэффициент теплоотдачи, Вт/(м·К)
для меди – 401 Вт/(м·К), алюминия – 202-236 Вт/(м·К);
Ватт на метр на кельвин Вт/(м·К) — производная единица в Международной системе единиц (СИ) для измерения удельной теплопроводности. 1 Вт·м⁻¹·К⁻¹ означает, что в материале один джоуль энергии в секунду (то есть, один ватт) передается на расстояние один метр вследствие разницы температур в один кельвин.
Иногда встречается: медь – 4.01 Вт/(см·°С), алюминий – 2.02-2.36 Вт/(см·°С)
Ватт на сантиметр на градус Цельсия Вт/(см·°С) — десятичная единица измерения удельной теплопроводности. 1 Вт·см⁻¹·°C⁻¹ означает, что в материале один джоуль энергии в секунду (то есть, один ватт) передается на расстояние один сантиметр вследствие разницы температур в один градус Цельсия.
Для подбора радиатора иногда проще воспользоваться следующим старым добрым графиком зависимости:
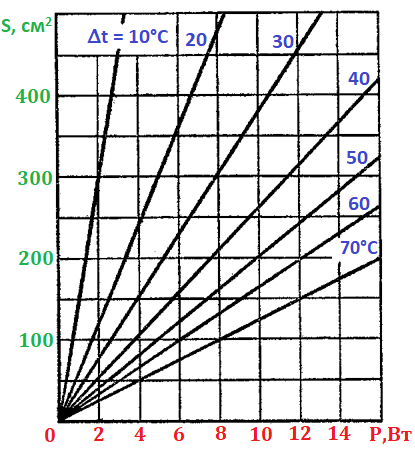
Зная разность температур, окружающая среда-радиатор (графики представлены с шагом 10°C от 10 до 70°C), зная рассеиваемую мощность (показана на горизонтальной оси), находим необходимую площадь радиатора, то есть общую площадь контакта радиатора с окружающим воздухом (смотрим по вертикальной оси).
Замечания о радиаторах
1. В схемах, где рассеиваются большие мощности, например, несколько сотен ватт, может понадобиться принудительное воздушное охлаждение. Для этого выпускаются большие радиаторы, предназначенные для работы с вентиляторами и имеющие очень низкое тепловое сопротивление от радиатора к внешней среде от 0,05 до 0,2 °C/Вт.
2. Типы радиаторов отличаются плотностью расположения ребер или игл. Для радиаторов с естественной вентиляцией расстояние между ребрами (иглами) должно быть не менее 4 мм. К тому же такие радиаторы рассчитаны для работы только в вертикальном положении, когда воздух под действием естественных сил движется между ребрами. Если расстояние между ребрами (иглами) составляет около 2 мм, то такой радиатор рассчитан на принудительную вентиляцию и требует установки вентилятора.
3. Если транзистор должен быть электрически изолирован от радиатора, особенно если несколько транзисторов установлено на одном радиаторе, то используют тонкие изолирующие прокладки между транзисторами и радиаторами. Также используют изолирующие вкладыши для монтажных винтов. Прокладки выпускаются под стандартные транзисторные корпусы и делаются из слюды, изолированного алюминия и двуокиси бериллия ВеO2. При использовании теплопроводящей смазки они создают дополнительное тепловое сопротивление от 0,14 °C/Вт (бериллиевые) до 0,5 °C/Вт.
Хорошей альтернативой могут служить керамические прокладки.

Изоляция таких прокладок выдерживает напряжение 22,5кВ при температуре до 1600°C, при этом у них отличная теплопроводность – 29,36 Вт/(м·К) (тепловое сопротивление 0,034 °C/Вт).
На китайских торговых площадках доступны также силиконовые прокладки разной толщины и размера с теплопроводностью 6 Вт/(м·К) (т.е. 0,16 °C/Вт).

Или самоклеящиеся прокладки, наподобие скотча. Ленты предлагаются шириной 10мм/15мм/20мм/25мм/30мм/40мм/50мм/80мм. Толщина 0,2 мм. Теплопроводность 1,2 Вт/(м·К) (0,83°C/Вт). Такую ленту удобно использовать для фиксирования светодиодов на одном радиаторе.

Если по каким-либо причинам у вас увеличился зазор между чипом и радиатором, существуют также специальные медные прокладки различной толщины от 0,1 до 1,5 мм. Прокладки помогут создать плотный переход.

4. Малые радиаторы выпускаются в виде простых насадок на малогабаритные корпусы транзисторов (подобные стандартному ТО 220). В случае малой рассеиваемой мощности (1–2 Вт) этого вполне достаточно. Не надо мучиться, монтируя транзистор куда то на радиатор, а потом тащить от него провода обратно к схеме.
Существуют различные типы малых радиаторов для работы с мощными интегральными микросхемами в пластмассовых корпусах (многие стабилизаторы, а также мощные транзисторы имеют такие корпуса). Эти корпуса монтируются прямо на плату на корпус интегральной микросхемы. Это очень удобно в схемах, где рассеивается мощность не больше нескольких ватт.

5. Иногда удобно монтировать мощный транзистор прямо на шасси или корпус прибора. В этом случае лучше использовать консервативный метод проектирования. Корпус должен оставаться холодным, так как нагретый корпус нагреет и другие элементы схемы и сократит их сроки службы.
6. Если транзистор смонтирован на радиаторе без изоляции, то надо изолировать радиатор от шасси. Применение изолирующих прокладок рекомендуется всегда. Конечно, если корпус транзистора не заземлен. Если транзистор изолирован от радиатора, то радиатор можно закрепить прямо на шасси. Но если транзистор выступает наружу из прибора (скажем, радиатор его смонтирован на внешней стороне задней стенки), то имеет смысл изолировать этот транзистор. Это нужно для того, чтобы никто до него случайно не дотронулся и не замкнул на землю.
7. Тепловое сопротивление «радиатор – внешняя среда» обычно указывается, когда ребра радиатора установлены вертикально и обдуваются воздухом без помех. Если же радиатор установлен как нибудь по другому или есть препятствия на пути потока воздуха, то эффективность радиатора снижается (повышается тепловое сопротивление). Лучше всего монтировать радиатор на задней стенке прибора, ставя ребро вертикально.
8. Поверхности радиаторов, да и транзисторов далеко не всегда зеркальные. Для заполнения мелких неровностей используют термопасту или специальный клей по консистенции похожий на термопасту. Термоклей удобно использовать для крепления небольших радиаторов или светодиодных матриц к радиатору, где не предусмотрен винтовой крепеж. Теплопроводность клея относительно не большая — 0,6716 Вт/(м·К). Клей наносится, как и термопаста, тонким слоем. Время на коррекцию 10 минут.
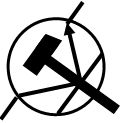
Сравнение китайских термопаст
В китайских магазинах по демократическим ценам можно приобрести термопасту GD66 в упаковках различных форм и размеров. Теплопроводность пасты – 1,05 Вт/(м·К), что соответствует термосопротивлению – 0,95 °C/Вт. У этой термопасты теплопроводность одна из худших, но она самая распространённая и дешевая. Самая лучшая теплопроводность у GD007 — 6,8 Вт/(м·К), но и цена на 50% выше.
Ниже представлена сводная таблица характеристик термопаст китайского производства: