Сигналы
Синусоидальные сигналы распространены наиболее широко; именно их мы извлекаем из стенной розетки. Если вы услышите выражение «10 мкВ на частоте 1 МГц», то знайте, что речь идет о синусоидальном сигнале. Математическое выражение, описывающее синусоидальное напряжение, имеет вид
U = A sin 2πft ,
где А – амплитуда сигнала, f – частота в циклах в секунду или в герцах.
Синусоидальный сигнал показан на рисунке
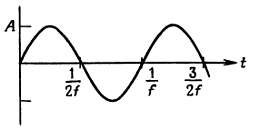
Если на входе линейной цепи действует синусоидальный сигнал, то на выходе также получим синусоидальный сигнал, но в общем случае его амплитуда и фаза будут другими.
Это утверждение справедливо только для синусоидального сигнала. На практике принято оценивать поведение схемы по ее амплитудно‑частотной характеристике, показывающей, как изменяется амплитуда синусоидального сигнала в зависимости от частоты. Усилитель звуковой частоты, например, имеет «плоскую» амплитудно‑частотную характеристику в диапазоне от 20 Гц до 20 кГц.
Частота синусоидальных сигналов, с которыми чаще всего приходится работать, лежит в диапазоне от нескольких герц до нескольких мегагерц. Для получения очень низких частот, от 0,0001 Гц и ниже, достаточно аккуратно построить нужную схему. Получение более высоких частот, например до 2000 МГц, также не вызывает принципиальных трудностей, но для сигналов такой частоты нужны специальные линии передач и специальные приемы передачи. Кроме того, здесь приходится иметь дело с микроволновыми сигналами, для которых не подходят привычные схемы, состоящие из отдельных элементов, соединенных между собой проводами, а нужны специальные волноводы.
Линейно‑меняющийся сигнал. Линейно‑меняющийся сигнал – это напряжение, возрастающее (или убывающее) с постоянной скоростью.
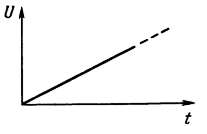
Это напряжение, конечно, не может расти бесконечно. Поэтому обычно такое напряжение имеет вид, показанный ниже, ‑ напряжение нарастает до конечного значения
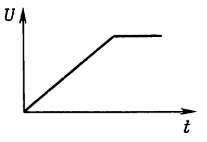
или на графике – пилообразное напряжение.
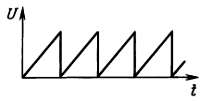
Треугольный сигнал приходится «ближайшим родственником» линейно‑меняющемуся сигналу; отличие состоит в том, что график треугольного сигнала является симметричным
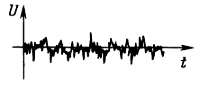
Сигналы шумов. Сигналы, о которых пойдет речь, очень часто смешивают с шумами, имея в виду только тепловые случайные шумы. Шумовые напряжения характеризуются частотным спектром (произведение мощности на частоту в герцах) и распределением амплитуд. Одним из наиболее распространенных типов шумовых сигналов является белый шум с гауссовым распределением в ограниченном спектре частот. Для такого сигнала произведение мощности на частоту в герцах сохраняется постоянным в некотором диапазоне частот, а вариации амплитуды для большого числа измерений мгновенного значения описываются распределением Гаусса. Шумовой сигнал такого типа генерирует резистор (шум Джонсона), и он создает неприятности при всевозможных измерениях, в которых требуется высокая чувствительность. На экране осциллографа мы видим шумовой сигнал таким, как он показан на рисунке
Прямоугольный сигнал. Как и синусоидальный, прямоугольный сигнал характеризуется амплитудой и частотой. Если на вход линейной схемы подать прямоугольный сигнал, то сигнал на выходе вряд ли будет иметь прямоугольную форму. Для прямоугольного сигнала эффективное значение равно просто амплитуде.
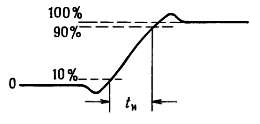
Форма реального прямоугольного сигнала отличается от идеального прямоугольника; обычно в электронной схеме время нарастания сигнала tн составляет от нескольких наносекунд до нескольких микросекунд. На рисунке ниже показано, как обычно выглядит скачок прямоугольного сигнала. Время нарастания определяется как время, в течение которого сигнал нарастает от 10 до 90 % своей максимальной амплитуды.
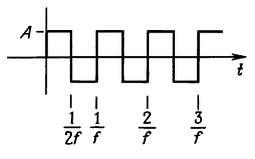
Импульсы. Импульсы характеризуются амплитудой и длительностью импульса. Если генерировать периодическую последовательность импульсов, то можно говорить о частоте, или скорости повторения импульса, и о «рабочем цикле», равном отношению длительности импульса к периоду повторения (рабочий цикл лежит в пределах от 0 до 100 %).
Импульсы могут иметь положительную или отрицательную полярность (пьедестал), кроме того, они могут быть нарастающими или спадающими. Например, второй импульс, показанный на рисунке, является убывающим импульсом положительной полярности (или спадающим импульсом с положительным пьедесталом).
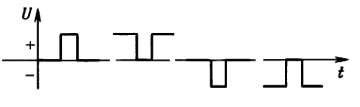
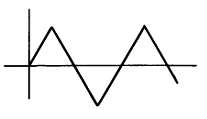
Сигналы в виде скачков и пиков. Сигналы в виде скачков и пиков упоминаются часто, но широкого применения не находят. К их помощи прибегают для описания работы схем. Если попытаться их нарисовать, то они будут выглядеть так, как показано на рисунке Скачок представляет собой часть прямоугольного сигнала, а пик – это два скачка, следующие с очень коротким интервалом.
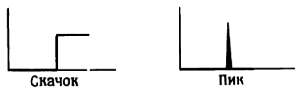
Логические уровни. Импульсы и прямоугольные сигналы широко используются в цифровой электронике. В цифровой схеме состояние любой точки в любой момент времени определяют заранее известные уровни напряжения. Эти уровни называют просто «ВЫСОКИЙ» и «НИЗКИЙ». Они соответствуют значениям «ложь» (0) и «истина» (1) булевой алгебры логики, которая имеет дело с переменными, принимающими эти значения.
В цифровой электронике точные значения напряжений не играют роли. Задача состоит в том, чтобы различать только уровни напряжения. В связи с этим для каждого семейства цифровых логических элементов определены допустимые значения высокого и низкого уровня напряжения. Например, логическое семейство цифровых элементов «74НС» работает от напряжения +5 В, при этом выходные уровни составляют 0 В (низкий уровень) и 5 В (высокий уровень), а порог срабатывания на входе равен 2,5 В. Реальные значения выходного напряжения могут составлять 1 В относительно «земли» или +5 В, но без учета ложного срабатывания.