АЦП. Методы преобразования. Преобразование напряжения в частоту, однократное интегрирование, двойное и многостадийное интегрирование, сигма-дельта
Данная статья является логическим продолжением статьи «АЦП. Параллельное кодирование, последовательное приближение». Как уже было сказано существует шесть методов преобразования аналоговых величин в цифровые, каждая со своими плюсами и минусами: параллельное кодирование, последовательное приближение, преобразование напряжения в частоту, однократное интегрирование, двойное и многостадийное интегрирование, сигма-дельта. В этой статье продолжим рассмотрение методов преобразования и рассмотрим оставшиеся.
Интегрирующие АЦП. Преобразование напряжения в частоту
Обзор принципов аналогово-цифровых преобразователей продолжат конверторы напряжение-частота (V-to-F или V/F). Здесь входной аналоговый сигнал преобразуется в непрерывный поток импульсов, чья частота пропорциональна уровню напряжения на входе. Импульсы можно получить, заряжая конденсатор током, пропорциональным входному напряжению, и разряжая затем до нулевого уровня. Для увеличения точности используется обратная связь. В одном варианте выход V/F-схемы сравнивается с уровнем на входе и поддерживается та частота, которая позволяет удерживать выход компаратора в нужном состоянии. В другой, более популярной схеме, используется метод «балансировки заряда».
Выходная частота преобразователей лежит в диапазоне от 10 kHz до 1 MHz для полного диапазона входных напряжений. Коммерческие преобразователи V/F имеют разрешение 13 разрядов (точность 0.01%) и являются примерами качественных генераторов, управляемых напряжением. Например, отличный AD650 фирмы Analog Devices имеет в рабочем диапазоне 0…10 kHz типовую нелинейность 0.002% . Он недорог и удобен для передачи по кабелю, когда требуется частота, а не цифровой код. Если скорость не важна, можно получать усреднённое цифровое значение, считая импульсы в течение определённого времени. Такая техника используется в простых цифровых щитовых приборах на 3 десятичных разряда.
Генераторы, управляемые напряжением, подобные AD650, являются асинхронными преобразователями напряжение-частота. Внутри у них есть постоянно тикающий генератор, а вывода для внешней частоты нет. Но задачу можно решать иначе. Можно пропускать на выход часть входного потока импульсов, пропорциональную в среднем входному аналоговому сигналу.
Для таких синхронных преобразователей V/F выходные импульсы появляются синхронно с внешней тактовой частотой. В каждом периоде тактовой частоты импульс может пропускаться на выход или блокироваться присутствовать или отсутствовать в зависимости от того, что требуется, чтобы средняя выходная частота была пропорциональна Vin. В общем случае расстояние между соседними импульсами постоянно меняется (но всегда пропорционально целому числу периодов тактовой частоты), т.е. на выходе нет какого-то регулярного сигнала. Выходная импульсная последовательность имеет «джиттер». Где-то, где усреднение сигнала внутренне присущее схеме свойство, это нормально. Например, так себя ведёт резистивный нагреватель с аналоговым датчиком температуры в контуре управления.
На рисунке показан усреднённый на промежутке длиной несколько секунд выходной сигнал, снятый на макете синхронного преобразователя V/F AD7741 с тактовой частотой 5 MHz .
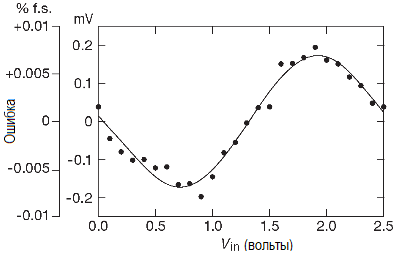
Линейность, как легко заметить, очень неплохая.
Синхронные преобразователи напряжение-частота являются простым примером «1-разрядного» АЦП. Есть и более удобные способы создания битовых последовательностей, пропорциональных среднему значению аналогового сигнала. А именно, сигма-дельта преобразователи делают подобную работу гораздо лучше. Но о них немного позже.
Интегрирующие АЦП. Однократное интегрирование
В этом методе однократного интегрирования внутренний генератор линейно возрастающего напряжения (источник тока + конденсатор) начинает цикл преобразования и одновременно запускается счётчик. Счетчик начинает накапливать импульсы стабильной тактовой частоты. Когда возрастающее напряжение сравняется со входным сигналом, компаратор остановит счёт. Полученная цифра и есть выходной код, пропорциональный входному напряжению. Блок-схема преобразователя показана на рисунке:
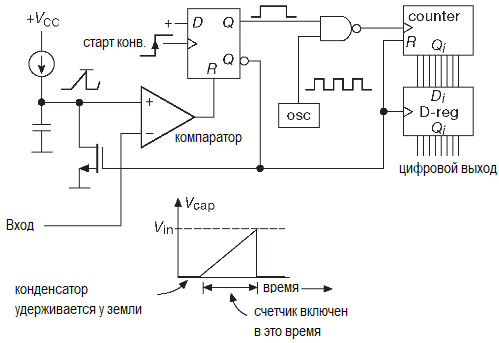
В конце цикла преобразования схема разряжает конденсатор и сбрасывает счётчик, после чего можно начинать новый цикл. Однократная интеграция проста, но не используется, когда нужна высокая точность, потому что накладывает жёсткие требования на стабильность и точность конденсатора и компаратора. Данное ограничение (и некоторые другие) отсутствует в методе «двойного интегрирования», который в настоящий момент используется везде, где нужны точные показания.
Однократные интеграторы живы и по-прежнему используются там, где абсолютная точность не требуется, но нужно равномерное разбиение диапазона по уровням. Примером может служить анализ амплитуды импульсов: пиковый детектор сохраняет максимальный уровень импульса, который затем преобразуется в адрес. Точное разделение по амплитуде является основным требованием для такой задачи, а метод последовательного приближения здесь совершенно не годится. Однократная интеграция используется также в преобразователях время-амплитуда.
Сетевые наводки
Есть несколько методов, использующих конденсатор для хранения соотношения между входным сигналом и опорным напряжением. Всё это — методы, усредняющие (интегрирующие) входной сигнал на фиксированном промежутке времени преобразования, что имеет два полезных свойства.
Использование одного конденсатора для сигнала и опорного напряжения позволяет не обращать внимания (до некоторой степени) на точность и стабильность ёмкости. Снижаются и требования к компаратору. Результат: при сравнимом качестве деталей точность выше, или можно получить такую же точность за меньшие деньги.
Выход пропорционален входному напряжению, усреднённому по фиксированному промежутку времени интегрирования. Если проводить интегрирование на промежутке, кратном периоду сетевой частоты, то преобразователь станет нечувствителен к сетевой наводке и её гармоникам во входном сигнале.
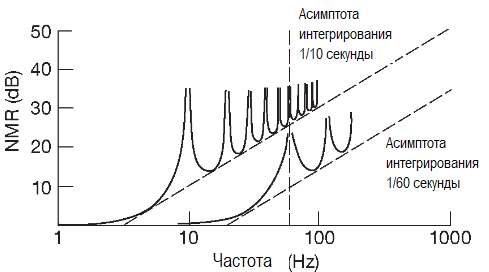
Избавиться от сетевой интерференции можно, только точно соблюдая пропорциональность времени интегрирования сетевой частоте, т.к. ошибка от даже доли процента сетевого периода приведёт к неполной компенсации наводок. Один из выходов — использование кварцевого генератора. Красивым вариантом будет фазовая автоподстройка для синхронизации рабочей частоты АЦП с сетевой частотой, снимающая все проблемы с подавлением наводок.
Недостатком интегрирующей техники является низкая по сравнению с последовательным приближением скорость преобразования.
Интегрирующие АЦП. Двойное и многостадийное интегрирование
Двойное интегрирование — красивая и активно используемая техника, которая позволяет избавиться от большей части проблем с конденсатором и компаратором. Основная идея представлена на рисунке.
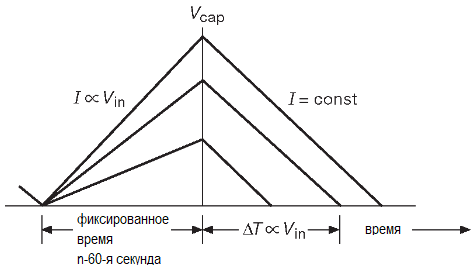
Сначала ток, точно пропорциональный входному напряжению, заряжает в течение определённого времени конденсатор. Затем конденсатор разряжается до нуля образцовым постоянным током. Время разряда пропорционально уровню входного напряжения и используется как сигнал разрешения счёта тактовых импульсов определённой частоты. Содержимое счётчика пропорционально входному напряжению.
Двойное интегрирование достигает очень высокой точности, не предъявляя жёстких требований к стабильности компонентов. В частности, не обязательно иметь точную величину ёмкости конденсатора, потому что цикл заряда и цикл разряда идут со скоростью, пропорциональной 1/C (и в уравнении взаимно компенсируются, т.е. сокращаются). Точно так же дрейф и смещение компаратора взаимно уничтожаются, т.к. конец цикла преобразования находится в той же точке и в тех же условиях, что и начало. В особо точных АЦП цикл измерения перемежается с циклом автоподстройки нуля, при котором на входе удерживается нулевое напряжение. Обе фазы проводятся одним и тем же интегратором и компаратором, поэтому вычитание результата «нулевого цикла» из результатов измерения полностью убирают все ошибки, связанные с нулевым уровнем, но не исправляют ошибок полной шкалы.
Отметим, что при двойном интегрировании не нужна даже особая стабильность и точность тактовой частоты. Время интегрирования в первой фазе формируется из целого числа циклов тактовой частоты. Если длительность цикла увеличится на 10%, то на столько же увеличится и уровень напряжения, которого достигнет напряжение на интеграторе. Значит, на столько же увеличится время полного разряда. Из-за того, что тактовая частота понизилась на 10% , число прошедших за время разряда циклов останется тем же! Единственная величина, требующая высокой стабильности в АЦП двойного интегрирования с автоподстройкой, — разрядный ток. Прецизионные источники напряжения и тока сделать относительно несложно, а уже он станет измерительным эталоном.
Преобразователи двойного интегрирования требуют высококачественных конденсаторов с наименьшей величиной диэлектрической абсорбции (эффект «памяти»). Наилучшими вариантами будут полипропиленовые, полистирольные и фторопластовые. Это неполярные конденсаторы, но внешнюю сторону фольги (она обозначается полоской) надо подключать к низкоимпедансной точке (выход ОУ интегратора). Чтобы минимизировать ошибки, значения R и C надо подбирать так, чтобы при измерении был задействован полный аналоговый диапазон интегратора. Высокая частота тактирования улучшает разрешение до тех пор, пока его период продолжает быть больше, чем время реакции компаратора.
При работе с АЦП двойного интегрирования (и вообще любого типа точных преобразователей) необходимо держать цифровой шум подальше от аналоговых цепей. В АЦП обычно имеется «аналоговая» и «цифровая» земля. Цифровые выводы АЦП очень полезно буферировать (например, с помощью ’541 — 8-канальных шинных формирователей и выводить их из Z-состояния только в момент считывания данных), отделяя от цифрового рёва микропроцессорной шины. В некоторых случаях приходится использовать оптические изоляторы. АЦП требуют хорошей фильтрации питающих линий в непосредственной близости от микросхемы. Да и вообще, следует поменьше шуметь в ходе преобразования, особенно в самый важный момент — вблизи точки срабатывания компаратора. Некоторые АЦП будто нарочно предоставляют пользователю возможность узнавать об окончании преобразования читая слово состояния. Так делать не надо! Используйте отдельную хорошо изолированную линию «BUSY».
Двойное интегрирование активно используется в цифровых мультиметрах. Этот метод недорог, точен и даёт хорошую повторяемость. Плюс он отлично подавляет сетевую наводку, да и другие виды интерференции тоже, а выходной код с ростом входного напряжения меняется строго монотонно. Но работает такой преобразователь медленно.
Стоит посмотреть на абсолютный рекорд среди интегрирующих АЦП — технику многостадийного интегрирования, придуманную фирмой Hewlett-Packard и реализованную в 8.5-разрядном вольтметре. Но сначала важный обзор методов использования аналоговых ключей.
Аналоговые ключи из стандартных логических семейств
Широко распространённые ключи ’4051 и ’4053 из состава семейства КМОП логики особенно удобны в аналоговых схемах, потому что у них есть линия отрицательного питания для аналогового канала и встроенные схемы сдвига уровней. Благодаря этому, микросхемы могут работать во всём диапазоне от -VEE до +VDD, а фактически заходя на 0.25 V за оба эти потенциала. Всего имеется три типа ключей. ’4053 — самый привлекательный (три независимых SPDT переключателя). ’4052 — пара мультиплексоров «4-в-1» и ’4051 (одиночный «8-в-1»). Привлекают они не только низкой ценой и большим числом производителей, но также высоким быстродействием и низкой ёмкостью.
Скажем, 74HC4053 имеет типичное сопротивление открытого канала 40 Ω, переключается за 20 ns и имеет ёмкость 8 pF. Если сравнивать её с микросхемами, официально предназначенными для переключения аналоговых сигналов, у ’4053 чуть меньший размах входного напряжения и нет защиты от статических разрядов (ESD). Если сравнивать с мощными КМОП переключателями, у ’4053 больше сопротивление открытого канала, но меньше ёмкость. Данный ключ хорошо вписывается в задачи переключения сигналов внутри одной печатной платы.
Одиночные версии SPDT ключей доступны в SOT23 и других компактных корпусах. Некоторые такие компоненты, например, ’1G3157 («1G» означает одиночный ключ) не имеют вывода отрицательного питания, поэтому не имеют обозначения «4053» в названии.
Рассмотрим парочку примеров, в которых ’4053 образует удобный мостик между цифровым и аналоговым миром. Второй пример с генератором пилообразного напряжения плавно переходит в тему преобразователей многостадийного интегрирования и сигма-дельта АЦП.
Программируемый генератор высоковольтных импульсов
Довольно удобно иметь генератор импульсов, сигнал на выходе которого можно включать логическим уровнем, и иметь независимую регулировку амплитуды. Последнюю задачу можно решать ЦАПом под управлением компьютера или набора ручек на панели. Простая схема делает всё изложенное, создавая сигналы с амплитудой до +100 V.
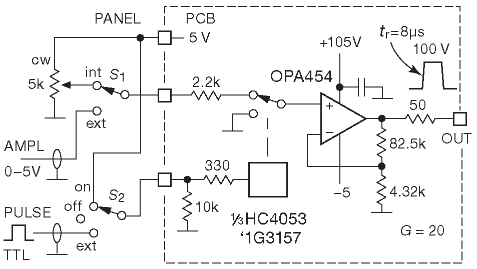
’4053 подаёт потенциал, выбираемый переключателем S1, на высоковольтный OPA454, включённый здесь неинвертирующим усилителем с G =20. ОУ не особо быстрый (время переключения около 10 μs), но зато недорог и может давать 100 mA в емкостную нагрузку. Его можно заменить на что-нибудь пошустрее, чтобы реализовать скоростные возможности ’4053 (∼20 ns). Переключатель со средней точкой S2 позволяет включать/выключать импульсы или подать на выход постоянный потенциал, чтобы проконтролировать амплитуду с помощью вольтметра.
Генератор пилообразного напряжения с переключаемым током
Схема использует очень хорошие характеристики аналоговых ключей ’4053.
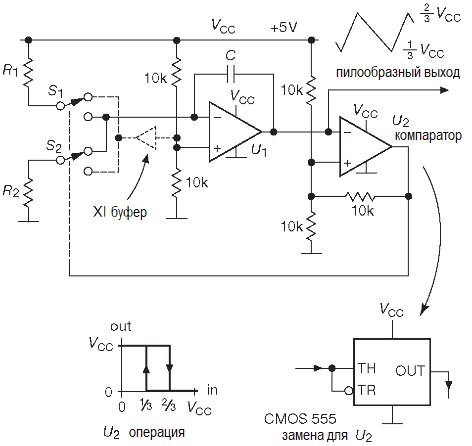
Предлагаемое переключение токов используется в АЦП многостадийного преобразования, который описывается немного дальше. Суммирующая точка интегратора на U1 заводится на среднюю точку источника питания (для работы от однополярного источника +5V). Ключи S1 и S2 типа ’HC4053, подключённые к тем же +5V, задают с помощью резисторов R1 и R2 наклон характеристики. Замыкание S1 включает источник VCC/2R1, вызывая спад напряжения интегратора, а S2 включает его рост. Пределы переключения компаратора равны 1/3 и 2/3 от VCC, ограничивая размах пилы величиной ΔV=VCC/3. Время роста напряжения равно tR=(2/3)R2C , время спада — tF=2/3R1C, а частота — f=1.5/C(R1+R2).
Скорости ключей и компаратора хватает для работы на частоте несколько мегагерц, для которой подойдут резисторы в килоомном диапазоне и конденсатор 100…500 pF. Такая ёмкость уже достаточно мала и заставляет думать об эффектах ёмкости ключей CSW, которые лежат в пределах 5…10 pF. Рассмотрим работу S1 в состоянии, показанном на схеме. Его ёмкость заряжается до +5V, после чего передаёт порцию заряда ΔQ=CSW·ΔV (где ΔV=VCC/2) в суммирующую точку, когда ключ перекидывается на нижний контакт. Такой перенос заряда вызывает скачок напряжения на выходе интегратора.
Средством борьбы с этим явлением будет удержание потенциала второго контакта на уровне суммирующей точки (часть схемы, нарисованная пунктиром).
Образцы для подражания: АЦП многостадийного преобразования фирмы Agilent
Учитывая предыдущий пример с аналоговым переключателем, разобраться с многостадийной техникой преобразования, применяемой в мультиметрах фирмы Agilent 34420 (7½ разрядов) и 3458A (8½ разрядов). Это старшие приборы инструментальных линеек Agilent, занимающие высшие ступени пьедестала уже более 20 лет. Упрощённый вариант схемы («Multislope III») используется в серии современных мультиметров, ставших промышленным стандартом — 34420 A (7½ разрядов), 34401A (6½ разрядов) и системе сбора данных 34970A (6½ разрядов). Здесь подробно разбирается работа схемы Multislope III и слегка затрагивается следующее поколение, явленное миру в 2006 — Multislope IV.
Основные принципы. Если коротко, то многостадийное преобразование стало развитием метода двойного интегрирования, т.е. многоциклового интегрирования с уравновешиванием заряда. Такой подход малочувствителен к параметрам конденсатора и учитывает накопленный остаток в конце цикла преобразования. В многостадийной технике сочетаются приёмы двойного и сигма-дельта интегрирования, а сама она является прямым переходом к сигма-дельта АЦП.
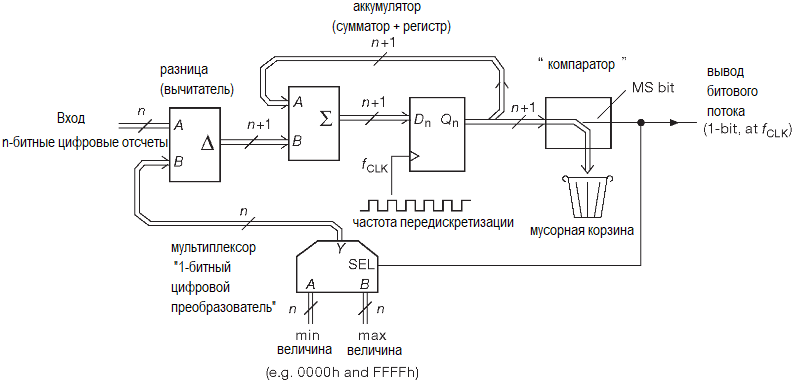
Блок-схема предельно проста и использует по большей части недорогие компоненты (исключая источники опорного напряжения и прецизионные резисторы).
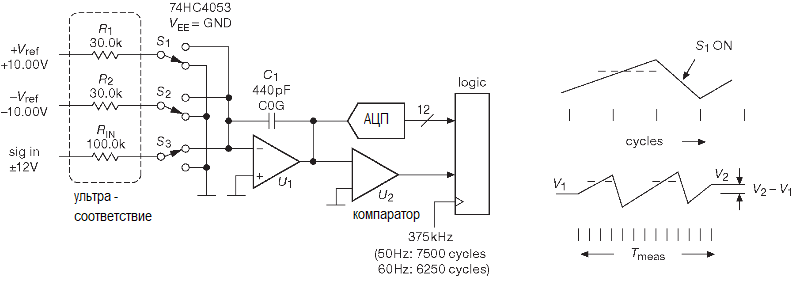
Схема включает интегратор U1, логическую часть, которая через компаратор U2 смотрит за выходом интегратора в каждом из тактов частоты 375 kHz и два ключа S1 и S2, балансирующие интегратор, закачивая и откачивая из него ток. АЦП с очень скромной точностью (12 разрядов) используется для считывания выхода интегратора в начале и конце общего цикла измерения.
Теперь, как это в принципе работает. Чтобы начать измерение, надо замкнуть ключ S3, что вызовет изменение напряжения на выходе интегратора вверх или вниз в соответствии с соотношением dV/dt= -Iin/C1= -Vin/Rin·C1. В каждом последующем такте системной частоты схема замыкает ключ S1 или S2 (согласно полярности напряжения на выходе интегратора), добавляя или вычитая образцовый ток от соответствующего опорного источника (±10 V/30 kΩ) и заставляя выход интегратора менять направление в сторону нулевого уровня. Это продолжается на протяжении достаточно большого числа тактов. Чтобы по максимуму подавить наводки от сетевой частоты желательно использовать в качестве системного времени какую-либо частоту, кратную сетевой, например, чтобы 6250 циклов соответствовало 1/60 или 1/50 секунды. В результате система получает число положительных (nP) и отрицательных (nM) циклов. Это даёт первое приближение среднего входного напряжения за время измерения.
Всё это пока не поражает точностью: при максимальном входном сигнале ±12 V получается nM – nP или ±2250 отсчётов, что соответствует 12-разрядному разрешению. А теперь следите за руками. Из-за того, что измерение продолжалось какое-то целое число тактов, не прерываясь событиями наподобие равенства нулю, как в двойном интегрировании, напряжение на интеграторе содержит дополнительные данные и позволяет провести уточнение дробной части результата, как это происходит в вереньерных шкалах. Именно для этого нужен 12-разрядный АЦП, изображенный на блок-схеме. Он используется для измерения уровня на интеграторе перед началом цикла измерения и по его окончании. Для 12-разрядного АЦП это даёт дополнительные 512 уровней разрешения внутри LSB исходной системы первого приближения, т.е. добавляет 9 бит к 12, полученным на первом этапе. В итоге получаем результат с точностью 21 разряд.
Для десяти циклов один цикл, он же «вереньерная часть» составляет 1/10, для ста — 1/100 и т.д. Для однотактного измерения всю информацию о сигнале будет содержать «вереньерная часть» ΔV.
Некоторые подробности. Это только общий обзор техники непрерывного преобразования. Здесь много о чём можно говорить: в деталях прячется целый табун дьяволов. Метод можно улучшать множеством доступных способов, добиваясь наибольшей точности в рамках исходной идеи. Здесь авторы наступят друг другу на горло и сократят комментарии до краткой выжимки из наиболее интересных и поучительных подробностей.
Некритичные компоненты
В качестве S1— S3 Agilent использовал обычные микросхемы 74HC4053 производства NXP, а в качестве C1 — массовый керамический конденсатор для поверхностного монтажа со стабильным диэлектриком NP0/C0G фирмы AVX. Этот тип конденсаторов очень дёшев, имеет малый температурный коэффициент 30 ppm/°C и пренебрежимо малую диэлектрическую абсорбцию (эффект «памяти»), особенно при таких временах переключения. Высокая точность и стабильность компаратора и АЦП тоже не нужна.
Критичные компоненты
Источник опорного напряжения устанавливает шкалу измерения и должен иметь высокую стабильность. В приборе используется один 7-вольтовый опорный источник на основе стабилитрона и два прецизионный операционных усилителя, чтобы получить 10.0 V опорного напряжения. Конкретная величина потенциала «10.0 V» неважна, т.к. будет учтена при калибровке, но это напряжение обязано быть стабильным, чтобы калибровочные значения как можно дольше отражали реальное положение вещей.
Ещё одним критичным компонентом является резисторная сборка R1 – R3 (масштабирующие резисторы в опорном источнике) и ОУ, на котором собран интегратор. Последний представляет собой композитный усилитель (OP27+AD711), имеющий высокое петлевое усиление в сочетании с низким напряжением смещения.
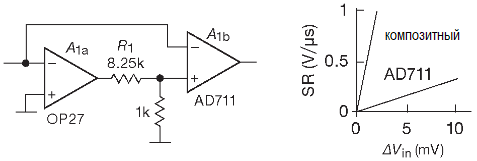
В качестве набора резисторов используется специальная точно подогнанная сборка, с хорошей стабильностью отношения. Здесь очень важен дрейф (по времени и температуре) отношения резисторов, потому что небольшое исходное расхождение также убирается заводской калибровкой.
Не показанный, но тоже важный, входной усилитель с программируемым усилением. Его усиление должно иметь высокую точность и стабильность, чтобы сохранять параметры настройки и калибровки.
Переключатели
Ключи 74HC4053 используются в схеме распределения тока. Ключи включены так, чтобы напряжения на всех выводах ключа поддерживались на близком к нулевому уровне. ’4053 используются только для переключения токов, чтобы повысить или снизить скорость роста напряжения на выходе интегратора, которая находится в точной зависимости от входного напряжения. Сопротивление открытого канала, конечно, оказывает на токи заметное влияние, но пока Ron ключей хорошо согласовано, стабильно и мало по сравнению с R1 – R3, его влияние можно учесть калибровочными циклами, которые прибор проводит в автоматическом режиме перед каждым измерением.
Для микросхем производства NXP, которые стоят в приборе, Ron имеет типовое значение 85 Ω и согласовано до 8 Ω. Очень важной особенностью является разрыв соединения перед переключением, благодаря чему выводы никогда не бывают закорочены (что замкнуло бы внутреннюю суммирующую точку на землю и проявилось бы на входе как дифференциальный сигнал, равный напряжению смещения ОУ). Одни производители упоминают данный факт в документации, другие — нет. Например, паспортные данные NXP указывают времена включения и выключения, разница между которыми и определяет время разрыва цепи 4 ns. Но прямо данное время не указывается, а, скажем, в справочных данных на DG4053 фирмы Siliconix есть параметр «Break-Before-Make Time Delay» tD=6 ns (тип.) или 2 ns (мин.).
Калибровка
Простая схема переключения токов очень удобна для калибровки и устранения эффектов неточного согласования резисторов, неточности опорного напряжения, смещений ОУ, задержек ключей и т.п. Например, когда S3 выключается (т.е. входной сигнал отсутствует), для S1 и S2 можно провести несколько последовательных циклов переключения. Накопившийся в результате этого действия потенциал ΔV на выходе интегратора отражает разницу положительного и отрицательного токов. По аналогии, подав на вход VREF, вместо сигнала, и проведя измерение можно выяснить отклонение опорных токов от номинальной величины. Перед каждым измерением с наибольшей точностью, когда разница имеет значение, прибор проводит серию таких калибровок. Естественно, обнаружить таким методом дрейф опорного источника нельзя. Чтобы поверять его, нужен внешний источник образцового напряжения, и на этом делают деньги поверочные службы.
Интервал измерений
Ранее в примере мелькала цифра Tmeas, равная одному периоду сетевой частоты или 6250 циклам частоты 375 kHz, или 1/60 (1/50) сек. Время измерения есть целое число циклов PLC (NPLC). Оно позволяет подавить наводку, а итоговая точность зависит от общей продолжительности цикла измерения. Но, согласно данным таблицы, можно делать быстрые измерения, если несколько поступиться точностью и степенью подавления сетевых наводок. Возможен также режим непрерывного измерения, при котором ключ S3 всегда замкнут (в этом режиме время измерения регулируется извне).
«Многомногостадийное измерение»
Вернёмся к исходному примеру — 8.5-разрядному мультиметру HP3458, в корне изменившему расклад сил. В нём есть четыре набора входных резисторов и ключей. Это позволяет очень сильно (почти в 600 раз) понизить скорость нарастания при приближении к моменту окончания измерения. Причём необычен отказ от использования красивого приёма — измерения остатка напряжения на интеграторе с помощью АЦП, а вместо этого проводится его линейный разряд до 0В.
Прочее
Остаётся ещё масса деталей итоговой реализации этой методики, которые описаны в руководстве по обслуживанию, статьях из HP Journal, и патентах. Например, данная техника предполагает только борьбу с насыщением интегратора, а значит, можно использовать больше одного компаратора и включать токовые ключи S1 и S2, только чтобы удерживать интегратор от насыщения. Это уменьшает число циклов переключения и связанных с ними ошибок. Есть и необычные схемные решения: ферритовые бусины на аналоговых входах ’4053 и конденсатор между суммирующей точкой интегратора и землёй.
Эволюция метода
В 2006 году Agilent представил более быструю линейку «Multislope IV» — модели 34410 A, 34411A и 34972A с USB и Ethernet на борту. Стоят они дороже, а цена на классические модели 34401A и 34970A была снижена. Заявлены модели 34460A и 34461A с графическими дисплеями и специальными интерфейсами для датчиков (34461A имеет такую же скорость измерения, как и 34401A). 34420 A замены не получил и остался единственным 7.5-разрядным (20 ppm) прибором в линейке.
От многостадийных к сигма-дельта. Многостадийные АЦП плавно подводят нас к очень широко используемой технике сигма-дельта преобразования, с которой имеют много общего. Оба используют интегрирование, при котором входной сигнал на периодической основе сравнивается с выходным напряжением интегратора. Как будет видно чуть позднее, в глубине сигма-дельта техники таятся некоторые тонкие отличия, позволяющие достигать фантастических параметров.
Сигма-дельта
Вот, наконец, дело дошло до самого лучшего метода аналого-цифрового преобразования — «сигма-дельта». Это довольно сложная тема, но, разобравшись в ней, можно понять, как достигаются параметры самых лучших по разрешению и точности (например, монотонность в диапазоне 31 разряда и более) «вольтметров» и звуковых ускорителей. Их архитектура с избыточной дискретизацией сильно упрощает входные спектральные фильтры и выполняет некоторые магические действия по удалению шума из рабочей полосы. И всё это за весьма скромные деньги. Сначала будут рассмотрены базовые принципы, а затем разобраны методы достижения гораздо более высоких параметров, нежели можно было бы ожидать.
Простая сигма-дельта система для подсчёта экспозиционной дозы солнечного света
Чтобы было с чего начинать, возвратимся к легенде пляжного приборостроения — мониторе экспозиционной дозы. Теперь экспонометр будет реализован на сигма-дельта интеграторе. Схема приведена на рисунке:
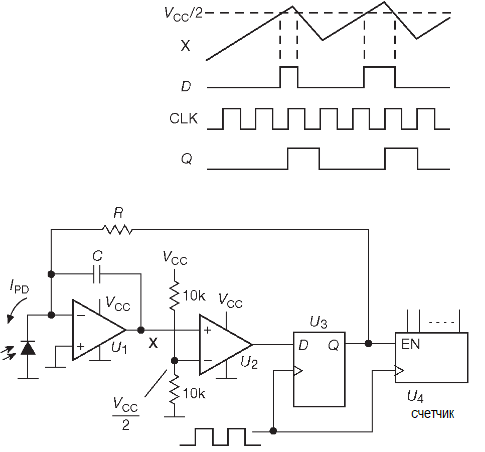
Используется вариант с синхронным дозированием заряда, который работает так же, как многостадийный интегратор. Такой способ проще, потому что не использует финальный уточняющий этап: общая доза солнечного освещения набирается простым подсчётом числа тактов, в течение которых потребовалось закачивать измерительный ток (здесь VCC/R), чтобы уравновесить вытекающий ток фотодиода IPD. Внешнее устройство сигнализирует, когда достигается установленный пользователем уровень. Сигнальная схема здесь не показана, но читатель, который знакомился с книгой последовательно, хорошо знает, как она может выглядеть.
Данное устройство представляет собой простейший сигма-дельта интегратор. Он накапливает (сигма) различия (дельта) между аналоговым входом и образцовым током, которые складываются в суммирующей точке. Оно может стать законченным аналого-цифровым преобразователем (а не простым интегратором), если добавить пару блоков:
- схему сброса перед началом работы
- элемент, считывающий показания счётчика на регулярной основе с интервалом, существенно превышающим период тактирования.
На самом деле схема может работать как АЦП и так, но на практике возможно достижение гораздо более высоких параметров, если простой счётчик заменить цифровым фильтром. Дальнейшего улучшения можно добиться каскадированием нескольких блоков «разностный усилитель — интегратор».
Все указанные улучшения будут внесены совсем скоро, но сначала надо разобраться, как работает этот простой пример.
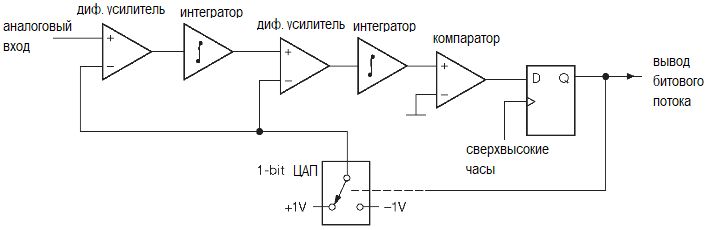
U1 — ОУ с однополярным питанием, который может работать с сигналами вплоть до отрицательного потенциала (и даже чуть ниже). U2 — компаратор с активной подтяжкой. В низкоскоростных схемах, подобных представленной, можно использовать сдвоенный RRIO усилитель LMC6482, который работает от тех же +3.3 или +5V, что и цифровые схемы, и очень нравится авторам. Напряжение на выходе интегратора растёт пропорционально току фотодиода IPD до тех пор, пока не превысит уровень VCC/2 . После прихода очередного активного фронта напряжение на выходе интегратора начинает снижаться со скоростью, пропорциональной общему току VCC/R -IPD. В результате активная часть периода (D), т.е. та часть цикла, когда его выход «Q» триггера U3 находится в состоянии ВЫСОКИЙ, усредняется по многим циклам: D=IPDR/VCC или IPD=DVCC/R. Длительность активной фазы цикла получается из числа N (содержимого счётчика U4 и времени измерения T, т.е. D= N/fclk T. Отметим, что результат не зависит от порогового напряжения компаратора (здесь VCC/2) или напряжения на выходе интегратора (точка «X»).
Ниже приводится правильная последовательность разработки.
Выбрать период тактирования, который гораздо короче, нежели ожидаемое время экспонирования, например, fclk=10 Hz. Можно и больше, но тогда потребуется более длинный счётчик.
Выбрать номинал R так, чтобы ток через него был больше, чем предполагаемый входной ток полной шкалы: для IFS=1 μA и VCC =5V номинал R должен быть меньше 5 MΩ .
Выбрать C так, чтобы изменение напряжения на выходе интегратора за время одного такта было меньше с некоторым запасом, чем уровень опорного напряжения компаратора.
Для схемы, изображенной выше, можно выбрать fclk =10 Hz, R=3.3MΩ, C =100 nF , при которых напряжение в точке «X» изменяется за время одного цикла не более, чем на 1.5 V (при минимальном IPD), а значит, не войдёт в насыщение. Пиковая частота счёта равна тактовой частоте, а средняя скорость счёта несколько ниже (здесь 0.6fclk), т.е. 16-разрядного счётчика будет достаточно для накопления экспозиционной дозы, эквивалентной двум часам солнечного света.
Несколько важных моментов.
Общая калибровка зависит от напряжения питания VCC, которое считается стабильным и равным +5V. Кроме того, в схеме используется способность КМОП логики достигать уровней питания.
Выходной сигнал интегратора не обязательно является периодическим. Он колеблется вокруг опорного уровня VCC/2, и единственное, что можно гарантировать, он изменит направление движения на следующем фронте, появившемся после пересечения уровня опорного напряжения. Такое поведение нисколько не снижает общую точность, усреднённую по множеству тактов. Метод интеграции сигма-дельта систем гарантирует их от переполнения любого вида.
Динамический диапазон преобразователя ограничен напряжением смещения ОУ, который вызывает появление ошибки входного тока Vos/R. Для схемы выше это 2nA в худшем случае для группы «-A». Входной ток ОУ (4 pA max при максимальной температуре) совершенно незначителен по сравнению с величиной ошибки от смещения.
Динамический диапазон можно сильно расширить, если заменить резистор R на переключаемый источник тока, предполагается, что входной сигнал остаётся токовым.
Точность компаратора U2 значения не имеет. Его вообще можно выкинуть, используя в качестве порогового входной логический уровень триггера. То же самое можно сказать о точности образцового напряжения: VCC/2 выбрано просто для удобства.
Всё, что вы хотели знать о сигма-дельта преобразовании, но стеснялись спросить. Как уже говорилось, сигма-дельта интегратор превращается в преобразователь среднего входного напряжения, если снимать накапливающиеся в счётчике числа на регулярной основе — с периодом Tmeas. Естественно, для достижения приличного разрешения время измерения должно быть гораздо больше, чем период тактовой частоты. Это означает, что если требуется АЦП со скоростью преобразования 100 ksps (период опроса со сбросом 10 μs), то для частоты 10 MHz максимальное число, которое счётчик сможет накопить за 10 μs будет равно 100, что чуть не дотягивает до 7-разрядной точности. Чтобы повысить её до 16 разрядов потребуется тактовая частота 216×100 kHz или 6.5536 GHz!
Это не вдохновляет. Идея «1-разрядного» АЦП оказалась дохлой, а весь выход — поток битов, которые можно засунуть в счётчик. Но ведь известно, что идея рабочая. Существует масса 16-разрядных сигма-дельта АЦП, оцифровывающих звуковой сигнал со скоростью 96 ksps. Есть даже 20- и более разрядные, работающие с такой частотой.
ΣΔ АЦП и ЦАПы
Как будет ясно из дальнейшего ΣΔ (или ΔΣ) преобразование может идти в любом направлении: как из D в A, так и обратно. В настоящее время ΣΔ ЦАПы используются в первую очередь в звуковой области, где очень важна их отличная линейность, монотонность и низкая цена. Типовой звуковой ΣΔ ЦАП может иметь шесть 24-разрядных 192 ksps каналов с эффективным динамическим диапазоном 114 dB. А ΣΔ АЦП закрывают широкий спектр применений от точных 24-разрядных медленных преобразователей до звуковых АЦП высокого разрешения (24 бита, 96 ksps) и быстрых преобразователей с невероятными параметрами (16 разрядов 20 Msps).
В дальнейшей дискуссии говорится преимущественно о ΣΔ АЦП как из-за их важности, так и из-за того, что в их конструкции находят применение близкие к идеальным цифровым фильтрам.
На этом пути придётся разобраться с вопросом, напоминающим большой розыгрыш, а именно:
«Как получается, что 1-разрядное преобразование, идущее с несколько более высокой скоростью дискретизации (скажем, в 64 раза большей, чем обычный предел Найквиста 2 fmax даёт на выходе цифровой код высокой точности, например, 16 разрядов?»
Мысль можно сформулировать иначе: от 1-разрядного преобразования с 64-кратной избыточной передискретизацией можно ожидать итогового цифрового кода с разрядностью 6 бит (26 =64), не больше. Дальше станет ясно, что это не просто возможно, но что можно достичь гораздо лучшего результата (именно это требуется в обработке звука).
Собственно процесс ΣΔ преобразования
Базовые этапы ΣΔ преобразования показаны на рисунке
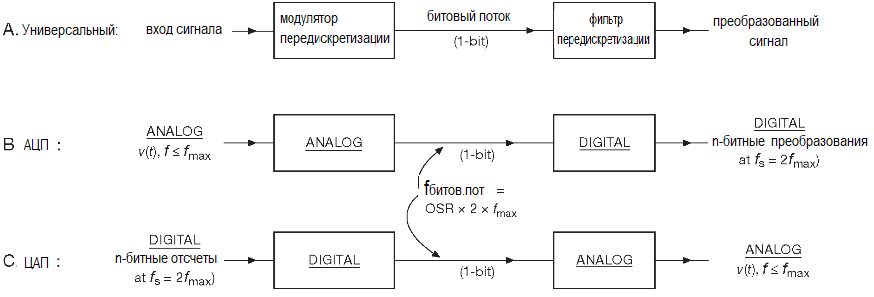
Входной сигнал с полосой, ограниченной частотой fmax (обычно это делается спектральным фильтром), преобразуется в битовый поток с помощью модулятора. Этот последний тактируется с частотой, кратной частоте предела Найквиста 2fmax, и даёт на выходе поток с частотой fbit = OSR × 2fmax, где OSR — коэффициент передискретизации. Битовый поток является только промежуточным этапом на пути получения результата: его ещё необходимо пропустить через ФНЧ.
Отметим, что и модулятор, и ФНЧ могут быть как аналоговыми, так и цифровыми. Тип зависит от конвертора: сигма-дельта АЦП состоит из аналогового модулятора и цифрового фильтра, а ЦАП — из цифрового модулятора и аналогового фильтра. Из сказанного следует, что сначала будет рассмотрен модулятор.
Модулятор. Так или иначе, но ФНЧ — это «просто фильтр», который ограничивает полосу входного сигнала. Всё самое интересное (и загадочное) творится в модуляторе. На рисунке приведена блок-схема передискретизирующего модулятора «первого порядка»
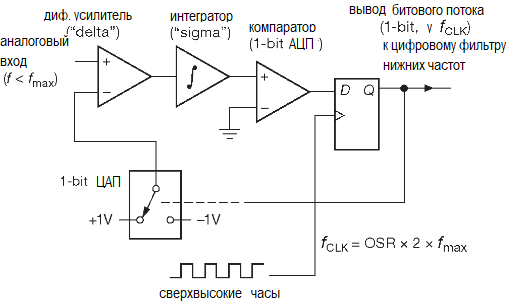
Модулятор получает на входе аналоговый сигнал амплитудой от –1 до +1V, лежащий в полосе с верхней границей fmax и создающий 1-разрядный битовый поток с частотой в OSR раз большей, чем предел Найквиста 2fmax.
В каждом цикле тактовой частоты текущее значение битовой последовательности, преобразованное в аналоговое напряжение (здесь ±1V), вычитается из входного сигнала, а разница интегрируется (самым обычным аналоговым интегратором, в данном случае неинвертирующим) и подаётся на компаратор с запоминанием. Усиление в интеграторе выбирается так, чтобы для сигнала полной шкалы на входе (здесь +1V) изменение выходного уровня за время одного периода тактовой частоты равнялось напряжению полной шкалы (+1V). Таким образом, интегратор можно рассматривать как «аналоговый аккумулятор»: для фиксированного входного напряжения V его выход увеличивается на V за один период тактового сигнала.
В результате получается быстрый поток нулей и единиц (на частоте, скажем, в 64 раза большей, чем обычная частота выборки 2fmax), соответствующий относительно медленному (в данном случае как минимум в 64 раза медленнее) изменению входного сигнала. Если условиться, что биты имеют уровень ±1V, получаем, что модулятор создаёт поток, чьё среднее значение соответствует входному сигналу. Данную схему можно рассматривать как петлю отрицательной обратной связи, которая стремится минимизировать среднюю (т.е. интегральную) ошибку между входным сигналом и выходным потоком (сравнение идёт в аналоговой форме, благодаря обратному преобразованию потока с помощью «1-разрядного ЦАПа»). Если взглянуть на схему внимательнее, то можно обнаружить, что происходит совершенно ужасная вещь: такт за тактом входной поток просто мечется между двумя предельными уровнями. Как точно заметил Боб Адамс: «Передискретизирующие преобразователи увеличивают разрешение не путём уменьшения ошибки между аналоговым входом и цифровым выходом, а заставляя ошибку появляться чаще.»
Динамический диапазон (разрешение) АЦП. Выходной цифровой ФНЧ создаёт цифровые n-разрядные числа, которые выводятся наружу. Используются обычно КИХ (FIR) фильтры.
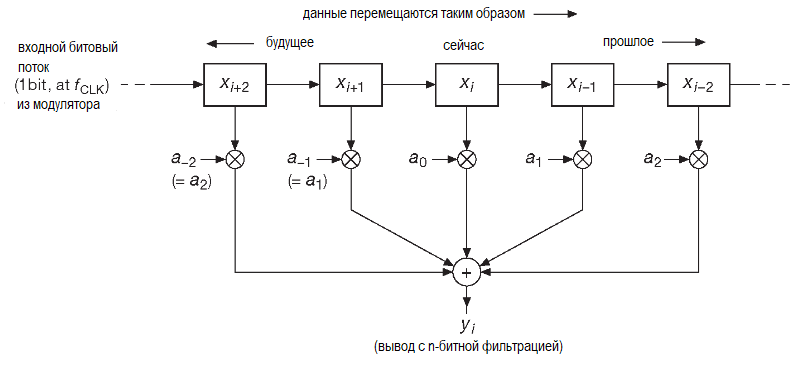
В этом случае 1-разрядный сдвиговый регистр с проходящими сквозь него единицами и нулями включает и выключает набор постоянных коэффициентов, которые суммируются с данными, получая в итоге n-разрядные выходные значения. Из-за того, что данные выходят из фильтра со скоростью передискретизации (т.е. в OSR раз быстрее, чем надо) их приходится подвергать прореживанию. Проще всего просто выкинуть лишние значения, оставляя только одно число на OSR тактов («###децимация»).
Если подойти к вопросу прямолинейно, то увеличение разрешения достигается усреднением массы 1-разрядных значений на каждой половине цикла наибольшей частоты входного спектра. Усреднённое значение битового поток отслеживает входной сигнал, и эта картина соответствует описанию Боба Адамса, а значит, всё хорошо.
Или не совсем? Рассмотрим пример: предположим, что оцифровывается звук с частотой fmax=20 kHz. Обычное АЦП (например, последовательного приближения) может работать со скоростью 48 ksps, оставляя удобный запас над предельной частотой 40 kHz. Теперь возьмём ΣΔ АЦП с типичным коэффициентом передискретизации 64, т.е. модулятор крутится на 64×48 kHz = 3.072 Msps, создавая 1-разрядный битовый поток с такой же скоростью. Фильтруем этот поток, допустим, фильтром «скользящего среднего». Цифровая фильтрация обрабатывает 64 последовательных бита одновременно. На что будет похож выход? Это просто. Когда усредняется 64 бита, на выходе может получиться только 64 65 возможных значений, т.е. в итоге получилось АЦП с разрядностью жалких 6 бит.
Каждый бит — отдельное значение, следовательно, усредняя сложением 64 однобитовых числа, получаем: если на входе все нули, выход =0, если все единицы =64. С мест поправляют: если есть состояния «0» и «64», то всего состояний 65.
Следуя той же схеме, чтобы достичь 16-разрядной точности, требуется обработать 216 = 65536 значений, что потребует выборки со скоростью приблизительно 3 гигагерца! Сигма-дельта преобразование, оказывается, не такая хорошая штука.
Что же происходит на самом деле? (Рассмотрение во временной области). Ответ на парадокс можно дать несколькими способами. В литературе по теме обычно говорится, что работа схемы квантования имеет две составляющие: идеальное преобразование и привнесение широкополосного «шума» (он состоит из разницы между реальным аналоговым сигналом и копией, восстановленной из получившейся 1-разрядной последовательности). Этот «привнесённый шум квантования» имеет широкий спектр (спасибо высокой частоте передискретизации), который заходит вверх за частоту тактирования. Важнее всего в этом процессе то, что шум квантования (который так и остаётся в выходных данных) минимален на низких частотах и растёт на высоких. Благодаря процессу модуляции большая его часть находится сильно выше fmax.
Полоса преобразования в 64 раза шире, чем 2fmax, а следовательно, даже при равномерном распределении шума в полосу сигнала с границей fmax попадёт 1/128 от общего шума квантования.
Такой спектральный состав позволяет выходному ФНЧ работать селективным подавителем большей части шума квантования в выходном потоке, сохраняя сам преобразованный сигнал. В итоге имеем гораздо большее разрешение и динамический диапазон, чем ожидалось при «тупом» рассмотрении процесса.
Приведённые выше рассуждения достаточно корректны, но не вполне удовлетворительны. Хотелось бы рассмотреть секреты динамического диапазона АЦП во временной области, не затрагивая частотную. Но в данном месте вышла некоторая заминка. Чтение опусов с названиями «Сигма-дельта АЦП раскрывают тайны» и «Сигма-дельта АЦП для идиотов» не помогло. Все такие публикации имеют слабое место: «..сигма-дельта преобразователи преодолевают данное ограничение с помощью техники сдвига шума..» и «..можно увидеть, как модулятор сдвигает шум в область высоких частот, позволяя получить более высокое разрешение» (выдержки из обеих указанных статей).
Вот как можно объяснить всё это в терминах временной области. Во-первых, ФНЧ не просто усредняет серию импульсов из живого битового потока. Вместо этого, он взвешивает каждое 1-разрядное значение с аккуратно подобранным коэффициентами, чтобы достичь наилучших параметров фильтрации. Из-за того, что отдельные отсчёты получают различный вес, появляется гораздо больше вариантов, чем просто 64 значения как в примере выше. Более того, типичный КИХ фильтр взвешивает и суммирует гораздо больше отсчётов и за гораздо большее время, чем период частоты передискретизации, т.е. уходя далеко за «интервал Найквиста» (под которым подразумевается половина периода частоты fmax). Для 64-кратной передискретизации можно использовать цифровую фильтрацию по тысячам точек (отдельным последовательным значениям внутри битового потока) каждый со своим множителем, размазывая каждый по десяткам интервалов Найквиста, чтобы получить в итоге окончательное (прореженное) число. Такой вариант достижения высоких разрешений как минимум несколько правдоподобнее, чем простое усреднение.
Продолжая в том же ключе, то, что каждый бит потока влияет на много прореженных итоговых n-разрядных выходных слов, ничего не означает. С конспирологической точки зрения, вполне правдоподобна версия, что модулятор столь умно придуман, что может создавать такой поток битов, который после прохождения через фильтр нижних частот преобразуется в n-разрядные выходные числа с очень сильно улучшенным динамическим диапазоном. То есть, не будет большой ошибкой сказать, что «всё дело в волшебном модуляторе». Но тогда вопрос надо ставить иначе: «Как столь примитивная железка (аналоговый сигма-дельта модулятор) может решать столь сложную задачу?»
Как уже отмечалось, обычно при описании сигма-дельта преобразователей говорят о «перераспределении шума» в частотной области. «Шум квантования» с плоским спектром, появляющийся в дискретизаторе «выдавливается» в область высших частот. По большей части в зону за пределами частоты выборки. Меньшее количество внутриполосного шума ведёт к увеличению точности. Вот, собственно, и все объяснения.
Итак, в сигма-дельта АЦП первого порядка шум квантования ослабляется на низких частотах, его спектр линейно расширяется вплоть до частоты передискретизации. Но частота-то избыточная, т.е. интересующий пользователя спектр расположен в низкочастотном углу (и занимает полосу согласно степени передискретизации). Другими словами, большая часть шума квантования лежит за пределами полосы сигнала. В модуляторах высоких порядков данный эффект проявляется отчётливее: график шума в модуляторе второго порядка квадратичный, кубический для третьего и т.д. Отсюда и процитированное заключение: «Сигма-дельта АЦП достигают такой точности, выдавливая шум в область высоких частот». Возможно, формулы не слишком возбуждают, но, по крайней мере, они показывают, что происходит в простой и однозначной форме.
Собственно процесс ΣΔ преобразования
И из правдоподобных аргументов во временной области, и из прямых расчётов в частотной выходит, что модулятор является ключом к высоким параметрам сигма-дельта АЦП. В их число входит способность оцифровывать аналоговый сигнал с разрешением заметно более высоким, чем коэффициент передискретизации. Более того, данный показатель растёт по мере роста сложности модулятора. Современные АЦП используют модуляторы «высоких порядков», что означает, единственный разностный усилитель и интегратор заменяется несколькими последовательными звеньями из разностного усилителя и интегратора каждое. Все звенья используют общий битовый поток
Модуляторы высоких порядков находят широкое применение, потому что расширяют динамический диапазон без увеличения коэффициента передискретизации. Кроме того, они в большей степени подавляют тон паузы, которые портят жизнь модуляторам первого порядка.
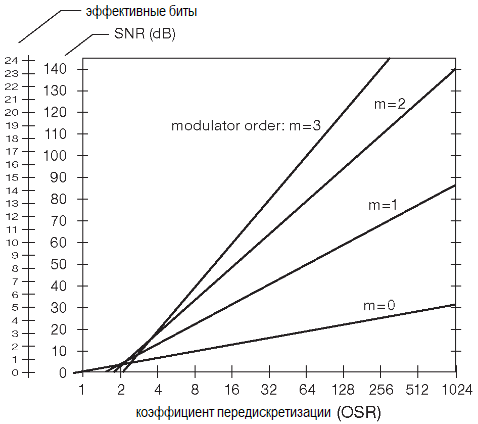
Хотя рассуждения о временной области могут быть полезны (разве что для обоснования заявленного отличного динамического диапазона), любая серьёзная аналитика должна использовать рассмотрение в частотном диапазоне. Последний показывает, что модуляторы высоких порядков (собранные на m интеграторах) изменяют спектр шума так, что внутриполосный шум квантования (от постоянного тока доfmax) подавляется в степени OSR [m+0.5], где m — порядок модулятора. Или иначе, каждое удвоение коэффициента передискретизации снижает шум квантования в такой степени, как если бы динамический диапазон увеличился на m+1/2 бита. График показывает теоретически возможный динамический диапазон сигма-дельта АЦП как функцию от коэффициента передискретизации и порядка модулятора.
Другим способом увеличения динамического диапазона, скорости или обоих параметров разом является построение модулятора, создающего поток «слов», каждое из которых имеет разрядность больше одного бита.
Моделирование
Предположим, есть желание увидеть, как сигналы проходят через сигма-дельта АЦП. А именно, хочется получить поток битов из случайного аналогового сигнала и итоговые числа (изображаемые в виде точек на одном графике с входным сигналом), причём делать это в частотной области, где перераспределение должно быть хорошо заметно.
Подобную задачу можно решить в пакете Mathematica®, используя следующие шаги.
Создаётся псевдослучайный сигнал с плоским спектром и гауссовым распределением амплитуд и выводится для 8192 последовательных промежутков времени.
Отфильтровывается идеальным ФНЧ со срезом на уровне 1/8 от исходной частоты и нормализуется, чтобы амплитуда попала в диапазон ±1. Это будет «аналоговый входной сигнал». Максимальная частота полученного сигнала обозначается как частота Найквиста fnyq.
«Входной сигнал» превращается в поток битов со значениями ±1 с помощью моделирования передискретизирующего сигма-дельта модулятора первого порядка (в котором интегратор выполнен в виде отдельного цифрового аккумулятора). В примере взят коэффициент передискретизации 8×: частота тактирования будет равна fclk = 8 × 2fnyq fclk должна быть кратна 2fnyq.
Полученный битовый поток рассматривается как аналоговый сигнал и пропускается через ФНЧ с такой же характеристикой, как и фильтр на шаге (b), чтобы получить выходные отсчёты. Выходные отсчёты появляются с частотой 8× и требуют прореживания (например, использованием только каждого восьмого бита), чтобы превратиться в выходной сигнал АЦП с частотой 1× (т.е. в два раза большей, чем fnyq — максимальной частоты во входном сигнале).
На рисунке показан характерный кусок более длинного результата моделирования, иллюстрирующий картину во временной области.
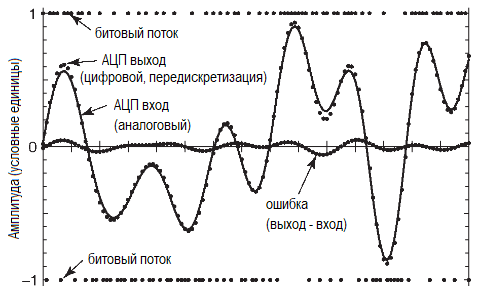
Отметки на горизонтальной оси соответствуют частоте 1× (пределу Найквиста), а отдельные точки следуют с частотой 8×. Входной сигнал — извилистая непрерывная линия, проходящая почти по точкам.
Отметки на горизонтальной оси соответствуют частоте 1× (пределу Найквиста), а отдельные точки следуют с частотой 8×. Входной сигнал — извилистая непрерывная линия, проходящая почти по точкам.
Точки — представление выходных чисел, в которых уже есть ошибка квантования, в аналоговом виде.
Поток битов показан там же в виде точек на уровнях ±1. Наконец, ошибка (цифровой выход минус аналоговый вход в каждой точке тактовой частоты 8×) — линия точек малой амплитуды. По этим графикам можно на глаз прикинуть точность преобразования. Здесь она составляет 6% от полной амплитуды и превращается в динамический диапазон SNR 16:1 или 24.
Из того же моделирования можно вывести частотный спектр входного сигнала и цифрового результата и разницу между ними (сигнал ошибки), см. рисунок
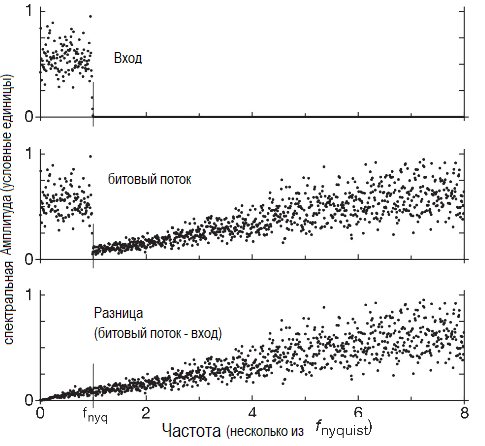
Спектр простирается до половины частоты передискретизации, т.е. до границы в 4 × 2fnyq (до 4×). Верхний график показывает плоский входной спектр, чётко срезанный идеальным фильтром на частоте fnyq. Средний график — спектр битового потока, в этом случае он рассматривается как аналоговое напряжение, которое предположительно содержит копию входного сигнала и какое-то количество шума квантования. Спектр простирается до частоты передискретизации (на рисунке обрезан на уровне «4×»). По рисунку видно, что картина соответствует ожиданиям: почти точное повторение спектра до частоты fnyq и дополнительный шум квантования, увеличивающийся пропорционально частоте. Чтобы оценить разницу, надо вычистить разность выходного и входного спектров — нижний график. Виден почти линейный рост от постоянного тока и до границы графика. Весь шум выше частоты fnyq будет вырезан выходным цифровым фильтром АЦП, через который проходит весь битовый поток. При этом фильтр работает с потоком как с набором цифровых значений.
Линейный характер спектра шума квантования в модуляторе первого порядка меняется на квадратичный в модуляторе второго порядка, и т.д. по мере роста порядка. Изменение характера графика соответствует улучшению точности (или SNR, или эффективному числу разрядов).
Что там у ЦАПов?
Как указывалось ранее, та же схема низкочастотной фильтрации битового потока, но порождаемого уже с помощью цифрового модулятора, используется в сигма-дельта цифро-аналоговых преобразователях.
В качестве входного сигнала такой модулятор принимает n-разрядные слова. Если сравнить его с аналоговым коллегой в АЦП, рассмотренном выше, то можно обнаружить, что разностный усилитель превратился в цифровое вычитающее устройство, а интегратор — в цифровой же аккумулятор. На каждом такте его текущее содержимое складывается с новым входным словом и вновь защёлкивается до следующего такта. Аналоговый компаратор заменён на цифровой вариант, который в наиболее простом случае передаёт далее по схеме знаковый разряд (или MSB в случае беззнакового кода со смещением). В этой точке образуется поток 1-разрядных слов, которые сообщают, больше или меньше середины шкалы было содержимое аккумуляторе. Наконец, 1-разрядный ЦАП заменило «n-разрядное АЦП», которое просто подаёт на сумматор максимальное или минимальное n-разрядное число, соответствующее выходному 1-разрядному значению в нужной кодировке. Для n-разрядного беззнакового кода со смещением это будут числа из n нулей или n единиц, т.е. для 16 разрядов — 0x0000 или 0xFFFF).
Так же, как и в случае аналогового модулятора в АЦП, цифровой модулятор в ЦАПе может иметь порядок отличный от единицы. Для этого надо каскадировать связку «вычитатель-аккумулятор» (т.е. цифровой ФНЧ). Так же, как и в аналоговой схеме, модулятор не ограничивается 1-битными выходными числами. Он может, и эта опция используется достаточно часто, выдавать поток многоразрядных слов. В таком варианте несколько старших битов направляются как в выходной поток, так и в цепь цифровой обратной связи. Для 2-разрядного модулятора (четыре уровня) 2-разрядные выходные слова будут:
преобразованы в 4-уровневый аналоговый сигнал (например, с помощью резистивного делителя), а тот, в свою очередь, пропущен через аналоговый ФНЧ, чтобы получить в итоге аналоговое выходное напряжение;
одновременно превращёны в одно из четырёх n-разрядных значений перекрывающих весь диапазон чисел (для 16 разрядов это могут быть 0x0000, 0x5555, 0xAAAA и 0xFFFF) и поданы обратно на входной вычитатель.
На выходе сигма-дельта ЦАПа как и на выходе сигма-дельта АЦП, стоит фильтр нижних частот. Но у ЦАПа это аналоговый фильтр, который лишён богатых возможностей цифрового варианта. Результатом является ухудшение характеристик: увеличение прохождения тактовой частоты на выход и чувствительность к джиттеру — дрожанию фазы тактового сигнала. Это обычная проблема «непрерывных» во времени линейных схем.
Плюсы и минусы ΣΔ конверторов
Достоинства.
Линейность, монотонность, точность
1-Разрядные сигма-дельта конверторы гарантируют монотонность, они изначально линейны и спокойно достигают точности 24 разряда на звуковых частотах.
Дешевизна
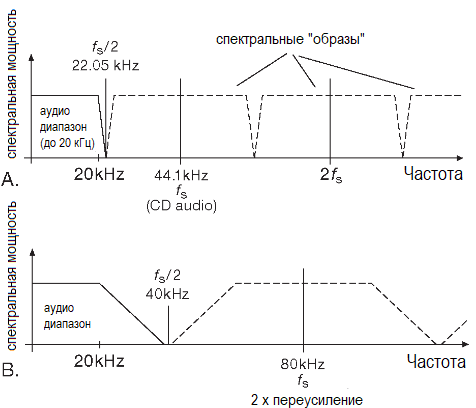
Сигма-дельта АЦП используют недорогую и точную цифровую фильтрацию, а благодаря передискретизации, нуждаются в простом аналоговом спектральном фильтре на входе.
Недостатки.
Ограниченная полоса
Верхняя граница ∼10…100 Msps определяется тактовыми сигналами в гигагерцовом диапазоне.
Задержка
Встроенный в АЦП выходной цифровой фильтр имеет идеальную почти вертикальную заграждающую характеристику за счёт использования большого числа точек (последовательных первичных отсчётов АЦП, участвующих в получении результата). И по той же причине он имеет большую задержку или «латентность», измеряемую десятками периодов выборки, т.е. в случае звуковых АЦП миллисекундами.
Шум ЦАПов
Сигма-дельта ЦАПы используют аналоговые выходные фильтры, которые пропускают на выход какое-то количество цифрового шума, полностью отсутствующего в R-2R ЦАПах.
Тон паузы
АЦП с модулятором первого порядка могут создавать «тональные паузы», когда получают на входе постоянный сигнал (и вызывают этим истерику среди аудиофилов). В модуляторах более высоких порядков такой проблемы нет: шум давится за счёт действия обратных связей более высокого порядка.