АЦП. Параллельное кодирование, последовательное приближение
Насчитывается немало основных способов аналого-цифровых преобразователей (АЦП), каждый из которых обладает своими преимуществами и ограничениями. Дабы не «утяжелять» страницу, в рамках данной статьи рассмотрим только два из них. Другие способы рассмотрим отдельно. Прямо сейчас не будем углубляться в подробности самого процесса преобразования. Сконцентрируемся на общих вопросах, в числе которых: параметры (скорость, точность и т.п.), цифровой интерфейс (параллельный или последовательный, однополярный или дифференциальный и т.д.), степень интеграции (один или несколько инверторов в корпусе, отдельный или встроенный в микроконтроллер или систему на кристалле).
В большинстве случаев дело приходится иметь с готовыми АЦП-модулями или ИС, а не строить что-то своё. Но важно понимать, как работают различные методы аналого-цифровых преобразований, чтобы случайно на попасть в хитрую ловушку, свойственную какому-то конкретному варианту.

Оцифровка: наложения, частота выборки и глубина выборки
Оставим разные ненадолго скучные подробности АЦП и разберёмся с выборками, которые будут постоянно встречаться, когда дело дойдёт до знакомства с методами аналогово-цифровых преобразований.
При конвертации аналогового сигнала (например, звуковой волны) в последовательность цифровых величин (т.е. цифр, соответствующих мгновенному значению напряжения в последовательные моменты времени) нужно уметь выбирать как точность измерения напряжения (глубину выборки), так и частоту, с которой делаются выборки.
Глубина выборки. Рассмотрим сначала глубину выборки и эффекты, с ней связанные (потому что их проще понять). Разбиение по 2n одинаковым уровням (n разрядам) ограничивает динамический диапазон величиной (6×n) dB. Форма сигнала, прошедшего такую операцию с учётом того, что он занимал полный диапазон преобразования, будет искажена. Сигнал получит шумы квантования (в ходе округления до ближайшего уровня квантования) на уровне 2–n (т.е. 100/(2n) процентов).
Например, 16-разрядное квантование звука (стандарт, используемый в звуковых CD) ограничивает динамический диапазон величиной 96 dB и минимальным уровнем искажений 0,0015%.
Если учесть, что реальный сигнал одновременно и ограничивается по динамическому диапазону, и получает увеличенные искажения, становится понятно, что хорошо спроектированная система должна иметь достаточную глубину квантования (и частоту выборки), чтобы не слишком ухудшать качество сигнала.
На следующем уровне подробностей есть кое-что ещё помимо числа разрядов: нелинейность (немонотонность), шум, помехи и т.д. Все они вносят «посильный вклад» в качество оцифрованного сигнала. Наиболее полный показатель, учитывающий большую часть указанных проблем, «ENOB» — эффективное число битов. О нем чуть позднее.
Частота опроса и фильтрация. Этот вопрос несколько сложнее (и интереснее). В противоположность интуитивным ожиданиям, сигнал, оцифрованный с частотой, более чем вдвое превышающей самую высокочастотную компоненту измеряемого спектра не имеет потерь информации. Ничего не теряется и в промежутках между точками измерения. Это наблюдение именуется «теоремой Найквиста» (и имеет свою группу противников, голосящих о душе музыки, которую убивают цифры).
Что же случится, если нарушить правило через субдискретизацию (т.е. с частотой, которая ниже требуемой согласно теореме). За ответом обратимся к рисунку, где синусоидальное напряжение с частотой 100 Hz, требующее fsamp> 200 sps, оцифровывается на скорости 90 sps, т.е. гораздо ниже предела Найквиста.
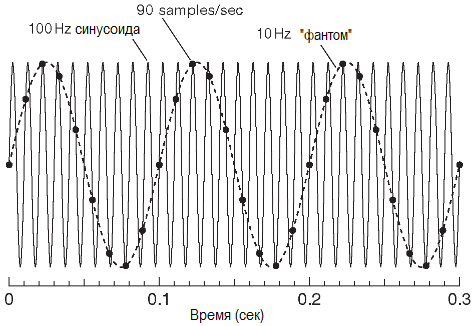
В результате отсчёты сложатся в фантомный сигнал (alias) с частотой 10 Hz. Т.е. мы получили разностный сигнал f100 Hz-fsamp=falias или выполнили сдвиг вниз по частоте. Именно он зовётся ложной низкочастотной копией сигнала (фантомная копия), и это совсем не то, что обычно хотят получить в ходе изменений. Проще говоря, для заданной частоты опроса fsamp аналоговый сигнал должен проходить через специальный спектральный фильтр, чтобы в спектре сигнала не осталось никаких существенных исходных составляющих с частотой, большей fsamp/2. Или иначе, для аналогового сигнала, занимающего полосу вплоть до частоты fmax, минимальная частота опроса должна составлять 2\fmax. Можно проводить выборку чаще, чем предписывает теорема Найквиста fsamp> 2\fmax, и это на самом деле достаточно разумно, потому что позволяет упростить условия фильтрации, как будет видно позже.
Очень полезно глянуть на последствия фильтрации в частотной области. На рисунке ниже широкополосный сигнал пропускается через неэффективный 2-секционный RC фильтр, в котором частота «-3dB» каждой секции равна пределу Найквиста (fsamp/2).
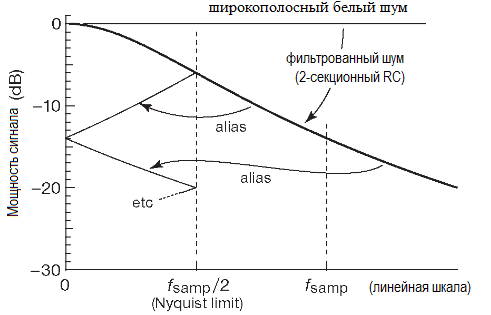
Частотные компоненты в запрещённой зоне ошибочно оцифровываются, как показано на рисунке, засоряя интересующую полосу сигнала. Убрать паразитные составляющие позднее нельзя: для цифрового сигнала эти компоненты уже внутриполосные.
Фильтр, защищающий от наложения спектров, с резкими срезами работает лучше, что видно на следующем рисунке, где показан фильтр Баттерворта 6-го порядка с частотой «-3dB», равной fsamp/2.
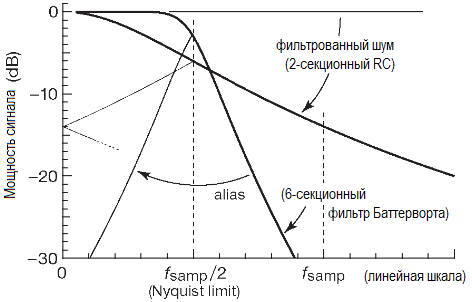
Но ситуация по-прежнему далека от идеала, и в сигнал попадает много посторонних гармоник. Особенно страдает высокочастотная область.
Остаётся только поднимать частоту опроса выше предела Найквиста, как на рисунке ниже, где частота опроса повышена на 25% относительно минимально необходимой для интересующей полосы.
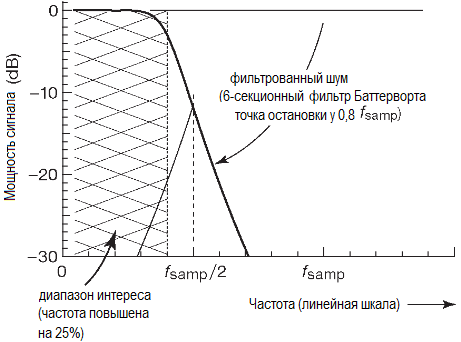
Это позволяет получить защитный зазор на переходе от полосы пропускания к полосе заграждения. Отметим, что частота «-3dB» фильтра равна верхней границе рабочей полосы, т.е. лежит ниже частоты опроса.
Именно так надо поступать, если интересует качество сигнала. Возвращаясь к аудио-CD с полосой 20 kHz, фильтр с вертикальными границами и частотой среза 20 kHz позволил бы проводить измерение с частотой Найквиста fsamp =40 kHz, но стандарт указывает величину 44.1 ksps (на 10% выше), что даёт защитный зазор шириной 20%.
Отметим свойственные спектральным фильтрам недостатки. Многозвенные аналоговые фильтры с резким переходом к заграждению, например, фильтр Чебышева, имеют плохие параметры во временной области: выбросы, звон, посредственные фазовые характеристики, чувствительность к номиналам компонентов и т.д.
Существует шесть методов преобразования аналоговых величин в цифровые, каждая со своими плюсами и минусами: параллельное кодирование, последовательное приближение, преобразование напряжения в частоту, однократное интегрирование, двойное и многостадийное интегрирование, сигма-дельта. В рамках этой статьи рассмотрим первые два.
Параллельное кодирование
Это, возможно, самый простой принцип построения АЦП, и одновременно самый быстрый. Входное напряжение подаётся одновременно на вход 2n одинаковых компараторов. В качестве опорных напряжений выступают потенциалы с 2n-стадийного делителя напряжения. Выходы компараторов образуют «термометрический» (линейный) код. Номер самого старшего сработавшего компаратора превращается приоритетным шифратором в n-разрядный выходной код. Следующий рисунок даёт концептуальное изображение данного метода.
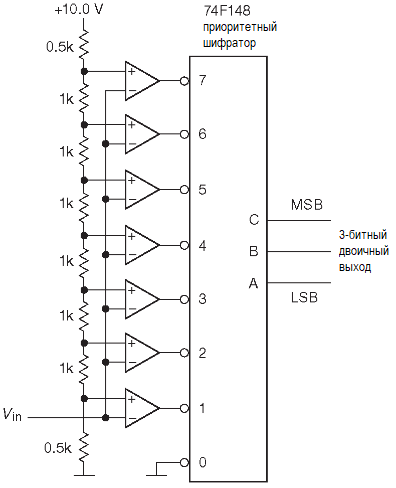
Здесь он реализован на дискретных компараторах и стандартной жёсткой логике. Собирать в «железе» именно эту схему не стоит, пусть этим занимаются производители кремния. В такой простой одностадийной схеме время задержки от входа до выхода равно сумме задержек компаратора, шифратора и выходного буфера (если он есть). Примером промышленной реализации именно такой схемы может служить MAX1003 — двухканальный 6-разрядный преобразователь, делающий 90 миллионов выборок в секунду (Msps) и имеющий задержку от входа до выхода один такт.
Модифицированная параллельная схема
В жизни простая параллельная архитектура была вытеснена модифицированными схемами: «полупараллельной», «субдиапазонной», «с интерполяцией» и «конвейерной». Новые варианты предполагают наличие шагов последовательного приближения или частичные преобразования. Таким образом, имеется некоторая задержка (или латентность) с момента выборки входного напряжения до появления выходного кода. Данное свойство не обязательно снизит максимальную скорость измерения. На самом деле обычно происходит ровно обратное явление: разделение общего процесса на несколько задач меньшей разрядности серьёзно повышает общую скорость.
Частично оцифрованные аналоговые остатки ещё движутся по конвейеру на основе конденсаторов, а АЦП уже начинает новое измерение. В таких преобразователях первая грубая прикидка (например, до двух старших разрядов) продолжается в каскадах последовательного приближения, работающих с остатками (разницей между входным напряжением и первым грубым 2-разрядным результатом). Так устроен ADC10D1500 — сдвоенный преобразователь на 1.5 Gsps в каждой секции (их можно включить попеременно и получить 10-разрядное АЦП со скоростью 3.6 Gsps). Его латентность — 35 тактов.
Возможно, самым простым вариантом такой конструкции является АЦП с частичным параллельным преобразованием полу-флэш. В нём измерение распадается на два участка. Первый — предварительная грубая параллельная дискретизация до половинной итоговой точности. Получение из этого результата с помощью внутреннего ЦАПа промежуточного аналогового напряжения. И второй этап — параллельное преобразование «ошибки» между входным напряжением и промежуточным потенциалом с выхода ЦАПа, на котором появляется младшая половина разрядов.
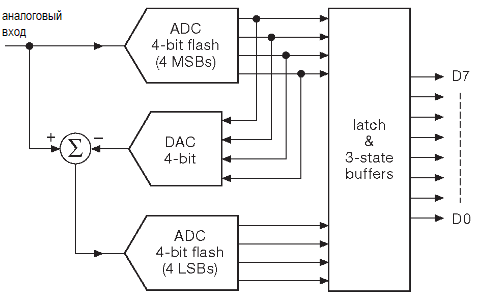
Более сложные АЦП используют схемы конвейерного типа, в которых аналоговые «остатки» от предыдущих этапов последовательно проходят цепочку относительно грубых преобразований. Скажем, AD9244 (ADI) использует 10-стадийный конвейер, чтобы получить 14-разрядов на 65 Msps с задержкой 8 тактов. AD9626 той же фирмы разменял точность на скорость: 12 разрядов, 250 Msps, 6 тактов задержки. Приведём цитату из его справочных данных:
«Конвейерная архитектура позволяет первому каскаду заняться новым преобразованием, в то время как другие каскады ещё обрабатывают предыдущие выборки. Каждый измерительный каскад, кроме последнего, состоит из грубого параллельного АЦП, подключённого к ЦАПу на переключаемых конденсаторах и межкаскадному усилителю. Усилитель масштабирует разницу между восстановленным напряжением на выходе ЦАПа и входным напряжением и передаёт её на вход следующего каскада конвейера… Последний каскад состоит только из АЦП.»
Такой же подход наблюдается в ADS5547 (TI) — 14-стадийный конвейерный АЦП, выполняющий 14-разрядные измерения на скорости 210 Msps с латентностью 14 тактов.
Архитектура с многодиапазонной параллельной дискретизацией достигает тех же целей (т.е. точного результата из грубых и уточняющих промежуточных значений), но более интересным методом. Он не требует конвейера и последовательных действий. Вместо этого входное напряжение проходит сквозь аналоговую схему размножения входного сигнала. Схема выполняется на цепочке перекрёстно включённых дифференциальных усилителей, которая отображает полное входное напряжение на множество одинаковых повторяющихся и соприкасающихся диапазонов. Грубая схема выбирает нужный диапазон (старшие биты), который затем оцифровывается с помощью параллельного АЦП (младшие биты). Выходное значение собирается из этих двух групп битов.
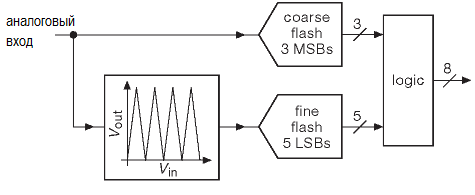
Такую технику использует серия «сверхскоростных АЦП» фирмы National Semiconductor/TI. На данный момент получены 12 разрядов на 3.6 Gsps (ADC12D1800).
Параллельные преобразователи используются в основном в дискретизации меняющихся сигналов, даже если общая скорость преобразования невелика. Все потому, что их высокая скорость (а точнее, малое апертурное время — длительность интервала выборки) гарантирует отсутствие изменения сигнала в ходе преобразования. Альтернативой им служат медленные АЦП. Они обычно нуждаются в схеме выборки-хранения, чтобы «замораживать» сигнал на время преобразования. Заметим, что будет или не будет латентность АЦП влиять на результат, зависит от конкретной схемы: что подходит осциллографу, то убьёт цепь обратной связи.
Входные схемы для параллельных АЦП
Современные АЦП несколько отличаются от первых простых преобразователей. Их возможности гораздо выше, но они капризные, их нельзя включать только на время измерений, и они очень зависимы от качества питания и цифровых линий связи. Теперь нельзя просто взять ОУ и подключить его к АЦП.
Покажем это на примере. На рисунке ниже изображён двухканальный 16-разрядный параллельный АЦП, способный работать на радиочастотах и идеально подходящий для оцифровки I- и Q-сигналов для радиосистем с программируемыми параметрами.
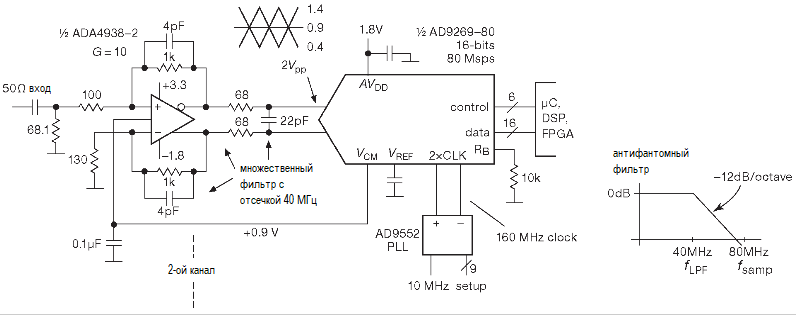
AD9269 — параллельный АЦП, но многие его проблемы свойственны и другим типам преобразователей. Некоторые сигма-дельта и схемы последовательного приближения требуют ставить на вход изолирующую цепочку из двух последовательных резисторов и параллельного конденсатора. Причём некоторые АЦП последовательного приближения, из которых пытаются выжать всё возможное, оказываются очень чувствительны к выбору номиналов этой троицы.
У 80-мегагерцовых АЦП предел Найквиста составляет 40 MHz и именно на такую частоту настроен входной дифференциальный 2R+C фильтр. Резисторы и конденсатор фильтра играют двоякую роль. Во-первых, АЦП отлично реагирует на любой шум (и белый, и прочие виды) в полосе вплоть до 700 MHz, поэтому выше 40 MHz выход буферного усилителя должен быть чист и тих. Во-вторых, входной схеме выборки-хранения преобразователя для нормальной работы требуется небольшая порция заряда, которая вытягивается из входного конденсатора. Два резистора, кроме того, изолируют выход усилителя от конденсатора, что очень важно, потому что 1000-мегагерцовый ОУ не переносит непосредственную емкостную нагрузку. Таковы три задачи для трёх вспомогательных компонентов, которых не было в старые добрые времена.
Зачем нужен усилитель c дифференциальным выходом? В общем случае на устройство с дифференциальными входами можно подавать однополярный сигнал на один вход и землю на другой. В современных АЦП такое включение заметно увеличивает искажения и ополовинивает рабочий диапазон (т.е. минус один разряд, а их и так мало).
Зато выбор дифференциального усилителя превращается в увлекательное времяпрепровождение. Если взять высокочастотные (500…1500 MHz) АЦП, то не удаётся найти микросхему с высоким входным дифференциальным импедансом «Zin diff ». Нужен дополнительный 40-мегагерцовый спектральный фильтр, который отсекает очень интересные варианты с внутренними резисторами установки усиления, потому что средние точки их делителей недоступны. И, наконец, требуется усиление не меньшее 10 или 20 dB. Поэтому в итоге был выбран ADA4938 (Analog Devices) с заявленной полосой 1000 MHz. Согласно графику его АЧХ величина GBW составляет 800 MHz, следовательно, f3db = GBW/G =80 MHz, а значит, на 40 MHz ещё останется запас по усилению.
Дифференциальные усилители подобной на схеме конфигурации, имеют довольно низкий входной импеданс, особенно это касается высоких усилений. Итак, с высоким входным импедансом дело не выгорело. А как насчёт вездесущих 50-омных источников широкополосных сигналов? Если выбрать Rg=100 Ω, то тепловой шум двух таких резисторов составит 1.8 mV/√fш т.е. будет гарантированно ниже, чем заявленный шум усилителя 2.6 nV/√fш.
Если поставить на входе 50-омный нагрузочный резистор, Zin не будет равен в точности Rg. В справочных данных приводится формула
Zin=Rg (1-Rf 2(Rg+Rf)
в соответствии с которой найден нагрузочный резистор 68 Ω. Затем с помощью резистора 130 Ω выравнивается импеданс на инвертирующем входе. Мероприятия по подгонке входного импеданса изменили коэффициент усиления Rf=GRg. Поэтому, чтобы сохранить G =10, приходится увеличивать Rf на 11%. Наконец, последний аккорд. Для перевода однополярного входа в дифференциальный требуется проверить полосу для «Vocm». По справочным данным частота «-3dB» для этого вывода усилителя равна 230 MHz. Значит, с учётом ослабления в цепи обратной связи частота «-3dB» для полного дифференциального диапазона АЦП сократится до 24 MHz.
АЦП AD9269 требует внешнего тактирования, и в схему добавлен совместимый генератор с фазовой автоподстройкой AD9552. Преобразователь позволяет поделить входную частоту пополам, чтобы получить внутренний тактовый сигнал с 50%-скважностью, чем стоит воспользоваться. Таким образом, для выборки с частотой 80 Msps требуется частота 160 MHz. Для опорной частоты 10 MHz требуется множитель 16. Сигма-дельта модулятор в AD9552 поможет при необходимости получить и дробные частоты, а у АЦП есть и другие коэффициенты пересчёта тактового сигнала.
Последнее предупреждение: джиттер. Графики в паспортных данных AD9269 сообщают, что для достижения самых лучших цифр отношения сигнал/шум (75…78 dB) джиттер тактового сигнала должен составлять не более 0.2 ps (или около 15 ppm за период измерения). Для PLL AD9552 этот параметр равен 0.11 ps, т.е. в данном случае условия выполнены (но запаса на вырост нет).
[Джиттер. Данное явление можно рассматривать как нестабильность на коротком временном интервале, в противоположность стабильности на длинном интервале, по которой определяются временные и температурные коэффициенты. Описанное неприятное свойство имеет множество имён, зависящих от контекста. Если речь идёт о синусоидальном сигнале в приложении к системам связи, то говорят о фазовом шуме или спектральной чистоте. Если же обсуждаются цифровые сигналы, задачи оцифровки и синтеза частоты или тактирование импульсных последовательностей, то речь идёт о джиттере].
Пример параллельного преобразователя с субдискретизацией
На следующем рисунке показана чуть упрощённая схема преобразователя с «субдискретизацией».
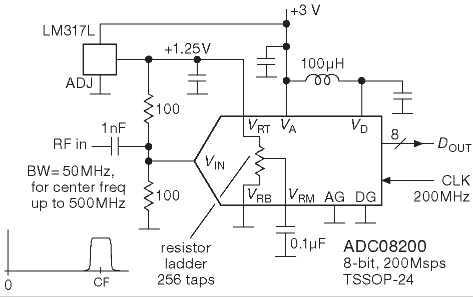
Интересующий сигнал группируется возле некоторой достаточно высокой частоты (скажем 500 MHz), а оцифровывается на скорости, которая значительно ниже, чем требуется по теореме Найквиста (например, 200 Msps). Такая схема будет работать, если выполнены два условия.
- Полоса сигнала должна удовлетворять критерию Найквиста, т.е. частота опроса должна как минимум вдвое превышать ширину рабочей полосы сигнала;
- полный спектр сигнала на входе АЦП (включая самые высокие его частоты) должен укладываться в рабочую полосу преобразователя по аналоговому сигналу.
Первое условие требует наличия чётких границ полосы сигнала, задаваемых обычно полосовым фильтром. Второе требование подразумевает, что АЦП изначально проектировался в расчёте на такое применение. ADC08200 на схеме имеет полную полосу пропускания по мощности 500 MHz, притом что максимальная скорость измерения составляет 200 Msps. Значит, подходит только для сигналов до 100 MHz. Описываемая схема дискретизации использует факт появления фантомных копий спектра в его цифровом представлении. Подход нормальный, но необходимо учитывать, что в рабочей области частот, куда происходит перенос спектра в ходе оцифровки, не должно быть никаких посторонних сигналов.
В данном примере использовался относительно низкочастотный параллельный преобразователь фирмы National Semiconductor/TI. Он работает от +3V, проводит измерение с частотой до 200 Msps, выводит 8-разрядные данные через простой параллельный порт. Его шкала преобразования состоит из 256 последовательных резисторов, требует внешней привязки потенциалов своих концов и обязательной развязки средней точки. Земля для нижнего и +1.25 V для верхнего потенциала. Катушка индуктивности на 100 μH отвязывает аналоговое питание «Va» от цифрового шума на выводе «Vd». С учётом строго положительного рабочего диапазона преобразования входной сигнал надо привязывать к его средней точке шкалы преобразования. Как показано на схеме. А пара 100-омных резисторов служит стандартной нагрузкой для радиочастотных сигналов.
Последовательное приближение
В классической технике последовательного приближения схема заводит текущий выходной код на ЦАП и сравнивает его выход со входным сигналом с помощью компаратора.
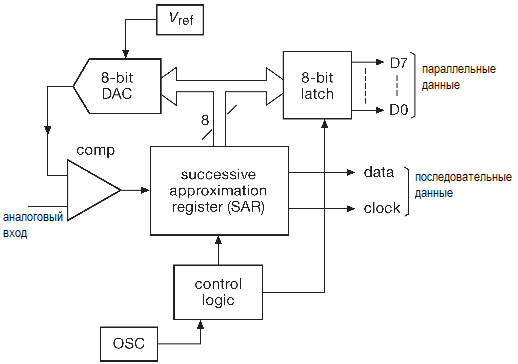
Процесс запускается с нулями во всех разрядах. Затем, начиная со старшего бита, очередной разряд временно переключается в единицу. Если выход ЦАПа при этом не дотягивает до входного сигнала, то данный разряд так и остаётся в единичном состоянии, в противном случае разряд сбрасывается, и цикл повторяется для следующего бита. Для n-разрядного АЦП требуется n тактов. В математике данная процедура носит имя двоичный поиск. АЦП последовательного приближения имеют вход «BEGIN CONVERSION» и выход «CONVERSION DONE». Результат может выдаваться параллельно (все разряды одновременно, каждый на своём выводе) или последовательно (n разрядов один за другим, начиная со старшего, через единственный вывод) или в обоих форматах одновременно. На рисунке показан выход ЦАПа, тактовые сигналы и признак окончания преобразования.
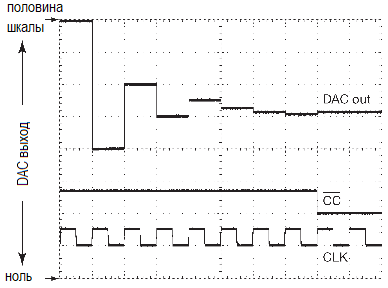
А на следующем рисунке — полное 8-разрядное «дерево» выбора, которое можно построить, наблюдая за выходом ЦАПа, когда на вход преобразователя подаётся линейно возрастающее напряжение, пробегающее весь входной диапазон АЦП.
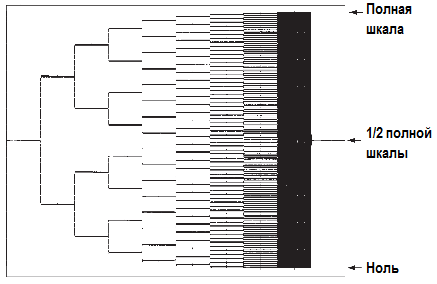
АЦП последовательного приближения занимают промежуточное положение по сочетанию скорости и точности (если сравнивать с быстрыми параллельными и точными, но медленными, «сигма-дельта» и интегрирующими вариантами). SAR модели требуют n периодов тактовой частоты для получения n-разрядной точности. Типичное время преобразования 1 μs, точность — от 8 до 18 разрядов. Преобразователи делают быструю выборку входного напряжения. Ошибка от его изменения (апертурная погрешность) может появиться только в этот момент, но импульсы на входе совершенно недопустимы. АЦП этого типа изначально достаточно точны, но требуют хорошо согласованных резисторных сборок. Они часто болеют странными нелинейностями и «пропущенными кодами». Одним из способов недопущения появления таких кодов является использование цепочки из 2n резисторов и ключей для создания промежуточных напряжений на манер ЦАПов на цепочке резисторов. Так работают 8-разрядные АЦП серии ADC0800 фирмы NSC/TI.
В современных АЦП последовательного приближения обычный резистивный ЦАП (цепочка R-2R резисторов) заменяется на ЦАП с перераспределением заряда.
Такая схема требует набора конденсаторов с двоично взвешенными емкостями, которые научились делать в кремнии и точно подстраивать. Таким образом, в 18-разрядном АЦП AD7641 имеется примечательный сам по себе набор из 18 конденсаторов номиналами C0, 2C0, 4C0…131072 C0. Конденсаторы на самом деле очень небольшие: C0 имеет номинал порядка фемтофарад (fF) или 0.001 pF.
Чтобы понять принцип работы, рассмотрим функционирование 3-разрядного преобразователя со схемы, представленной на рисунке.
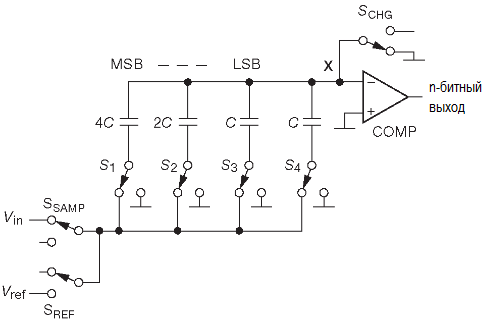
На рисунке ключи находятся в положении выборка, в котором напряжение на конденсаторах повторяет (отслеживает) входной сигнал.
- Ключ SSAMP размыкается, а конденсаторы продолжают хранить полученный заряд, т.е. копию входного напряжения.
- Размыкается ключ SCHG, и потенциал на входе компаратора теперь может меняться в соответствии с промежуточными цифровыми кодами, приложенными к S1-S3. Если, например, все ключи замкнуты на землю, то на входе «X» будет напряжение -Vin.
- Теперь, чтобы измерить значение хранимого напряжения Vin, зарядные ключи начинают переключаться один за другим. Сначала старший S1 подключается к +VREF (потенциал полной шкалы АЦП), а S2, S3 и S4 подключаются к земле. Такое действие добавляет на вход «X» смещение VREF/2 к уже имеющемуся -Vin (это емкостной/зарядовый делитель, который часто называют «делителем с перераспределением заряда»).
- На выходе компаратора в этот момент появляется старший разряд — HIGH, если Vin>VREF/2 , LOW в противном случае.
- Как в классической процедуре последовательного приближения ключ или возвращается к потенциалу земли или остаётся замкнутым на VREF, соответственно. После чего начинает проверяться следующий ключ. Для выяснения полного n-разрядного кода процесс повторяется n раз (здесь n=3).
Простой АЦП последовательного приближения
Использовать АЦП такого типа очень легко, как можно понять из рисунка.
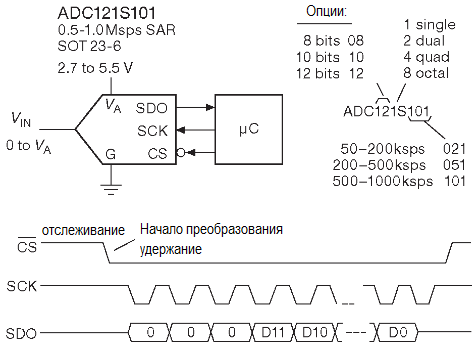
Последовательный интерфейс SPI сам по себе не сложен. Перевод «/CS» в активное низкое состояние запускает преобразование. Биты один за другим выводятся наружу по фронту сигнала «SCK», запуская одновременно преобразование для следующего бита. Такая схема позволяет держать линии последовательной связи в пассивном состоянии, минимизируя наведённый цифровой шум до момента активации «/CS». Указанные на схеме относительно низкочастотные преобразователи имеют внутреннюю схему выборки-хранения. Так же имеют три градации точности (8, 10 и 12 разрядов) и четыре вида упаковки (по одному, по паре, по четыре или по восьми АЦП в корпусе), итого, 36 вариантов. Одиночный преобразователь 1 MHz, 12 разрядов, в корпусе SOT23-6.
Вход АЦП часто совсем не похож на вход ОУ. Его импеданс может быть мал, а входная ёмкость, наоборот, довольно велика. На рисунке ниже приведена эквивалентная схема входных цепей преобразователя, где отчётливо виден конденсатор выборки-хранения величиной 26 pF, который будет заряжаться от измеряемой схемы.
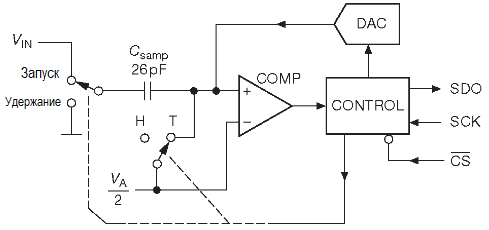
Если частота относительно низкая, такая нагрузка не особо обременительна, но её следует иметь в виду.
Варианты схемы последовательного приближения
Схема, известная как «следящее АЦП» использует реверсивный счётчик, чтобы получать последовательные промежуточные коды. Это замедляет реакцию на большие перепады сигнала, но зато отслеживает плавные изменения быстрее, чем схема последовательного приближения. Для большой разницы скорость нарастания пропорциональна тактовой частоте. Очередь реверсивных битов последовательна по своей природе и является упрощённой формой дельта-модуляции.
Ещё одним вариантом является дельта-модуляция с изменяемой крутизной (CVSD) — простой метод, который иногда используется для последовательного 1-битного кодирования речи, например, в беспроводных телефонах. В CVSD нули и единицы кодируют направление шага (вверх или вниз) формы выходного сигнала, но степень изменения текущего сигнала подстраивается в соответствии с его ближайшей историей. Например, величина шага, соответствующего 1 увеличивается, если несколько предшествующих битов также находились в состоянии 1 (длина необходимой последовательности зависит от установленных правил). Декодер, зная правило кодировки, может восстановить исходный сигнал. Раньше этот способ кодировки выполняли в кремнии, но сейчас он реализуется почти исключительно в виде программ для микроконтроллеров и DSP.
Пример включения АЦП последовательного приближения
Познакомимся с основными задачами для АЦП последовательного приближения: малошумящий 18-разрядный АЦП со стабильными параметрами и скоростью преобразования 2 MHz.
На схеме ниже показан типовой АЦП фирмы Analog Devices 18-разрядный 2 Msps AD7641 (фирменная линейка PulSAR). Он использует три положительных источника питания, которые, к счастью, можно включать в любой последовательности.
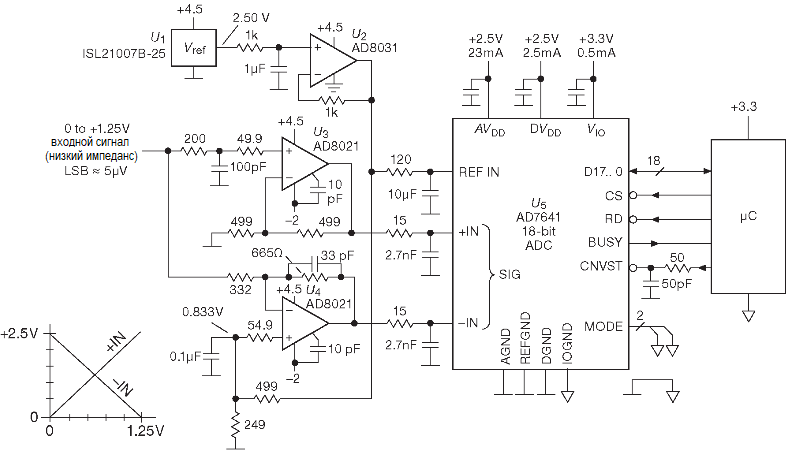
Входной диапазон AD7641 составляет ±VREF — это обычная величина для низковольнтых АЦП. Преобразование с минимальным шумом требует увеличения величины опорного напряжения и максимального соответствия входного сигнала полному диапазону измерения. Питание аналоговой части «AVdd» составляет +2.5 V, поэтому дифференциальный аналоговый сигнал ограничен величиной 0…+2.5 V. Если используется максимально допустимое опорное напряжение +2.5 V, то полная шкала будет ±2.5 V. Для дифференциального сигнала: когда «+IN» проходит путь от 0 до +2.5 V, «—IN» будет правильнее измениться от +2.5 V до 0, а иначе останется только 17 разрядов. Для 18 разрядов вес младшего составит 19 μV. Столь малые напряжения требуют внимательного отношения, особенно если частота опроса составляет 2 Msps, а полоса по уровню «-3dB» равна 50 MHz. Без должного обращения в ней немедленно появится масса шума от близлежащих цифровых цепей.
И входной сигнал, и опорное напряжение отлично воспринимают наводки от схемы перераспределения заряда, поэтому в схеме стоят стабилизирующие конденсаторы (справочные данные рекомендуют 2.7 pF), чтобы подавить шумы переключения. Операционные усилители не любят емкостную нагрузку, которая вместе с индуктивностью цепи обратной связи ведёт к самовозбуждению и звону, отсюда и последовательный резистор 15 kΩ. Получившийся RC фильтр имеет частоту среза 4 MHz и давит внеполосный шум. В такой полосе требования по плотности шумов снижаются и составляют всего 9.6 nV/√fш. Отметим заметное сопротивление (120 Ω) последовательного резистора в цепи VREF, призванного ограничивать бросок тока при включении питания, тем более что здесь широкая полоса не нужна.
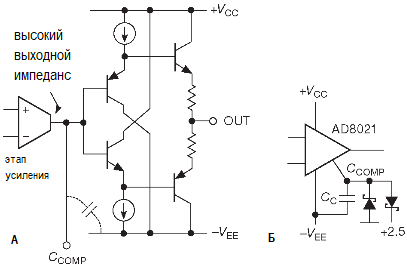
На схеме изображена обвязка, оптимизированная для работы в широком диапазоне частот с однополярным сигналом от 0 до +1.25 V. AD8021 — широкополосный малошумящий ОУ, рекомендованный в справочных данных на АЦП. Это, может, и не самый лучший компонент для использования, но продолжим следовать рекомендациям производителя. Пара ОУ создаёт точный дифференциальный сигнал из однополярного. Верхний каскад имеет усиление +2, а нижний -2. Отметим небольшие номиналы резисторов, которые позволяют иметь широкую полосу и низкий тепловой шум. Параллельная, а не последовательная схема получения дифференциального сигнала используется, чтобы выровнять задержки в обеих ветвях.
Ещё один приём: инвертирующий усилитель опирается на уровень VREF/3, чтобы получить требуемый диапазон от +2.5 V до 0. Обе ветви имеют разное усиление по шуму, но AD8021 позволяет добавить компенсирующий конденсатор 10 pF на специальный вывод, чтобы подсократить отклик и добиться примерно равных рабочих частот. Из-за высокого входного тока Ib =7.5 μA приходится выравнивать сопротивление цепей на инвертирующем и неинвертирующем входах ОУ. В данном случае это очень эффективный приём, так как типовой ток смещения AD8021 в 75 раз меньше входного и составляет всего 0.1 μA.
Опорный источник ISL21007/9BFB825 фирмы Intersil использует технологию плавающего затвора ПТ (т.е. заряд внутреннего конденсатора), что позволяет получить необычно низкий дрейф по времени. У него отличная начальная точность (0.02%) и низкий температурный коэффициент (3 ppm/°C). Источник снабжён противошумовым фильтром и буферным ОУ, который изолирует 3.3 mA тока нагрузки, чтобы снизить разогрев опорного источника. Усилители питаются от +4.5 V и -2.0 V, получаемых из ±5V для АЦП.
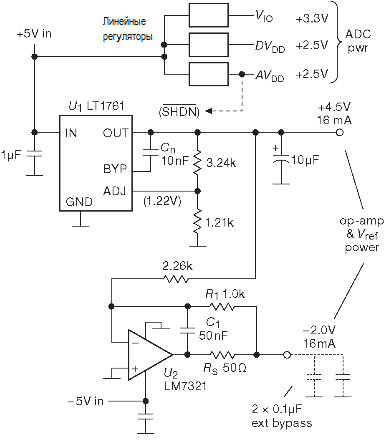
Поэтому усилители включаются одновременно с преобразователем, что минимизирует ток через ограничительные диоды на входе АЦП при подаче питания. Ещё один способ ограничить сигнал на входе АЦП — использовать специальный ОУ с ограничением AD8036, но его ошибка по постоянному току выше, чем у AD8021. К счастью, есть очень простое решение: поставить на вывод «Ccomp» микросхемы AD8021 два ограничительных диода Шоттки SD101 с малой ёмкостью (2 pF), один на землю, другой — на +2.5 V, как показано на рисунке.