Активные фильтры. Типы и сравнение фильтров

Простые RС‑фильтры верхних или нижних частот обеспечивают пологие характеристики коэффициента передачи с наклоном 6 дБ/октава после точки, соответствующей значению коэффициента передачи –3 дБ. Для многих целей такие фильтры вполне подходят, особенно в тех случаях, когда сигнал, который должен быть подавлен, далеко сдвинут по частоте относительно желательной полосы пропускания. В качестве примеров можно указать шунтирование радиочастотных сигналов в схемах усиления звуковых частот, «блокирующие» конденсаторы для исключения постоянной составляющей и разделение модулирующей и несущей частот.

Частотная характеристика RС - фильтров

Однако часто возникает необходимость в фильтрах с более плоским участком характеристики в полосе пропускания и более крутыми склонами. Такая потребность существует всегда, когда надо отфильтровать сигнал от близкой по частоте помехи. Возникает следующий очевидный вопрос: можно ли (соединяя каскадно одинаковые фильтры, скажем, нижних частот), получить аппроксимацию идеальной характеристики фильтра нижних частот типа «кирпичная стена», как это показано на рисунке

Простое каскадное соединение не дает результата без ухудшения общей характеристики, так как входное сопротивление каждого звена будет служить существенной нагрузкой для предыдущего звена. Но если поставить буферы между всеми звеньями (или сделать полное входное сопротивление каждого звена намного выше, чем у предыдущего) то, казалось бы, можно добиться желаемого эффекта. Тем не менее, ответ на поставленный вопрос будет отрицательным. Соединенные каскадно RС‑фильтры действительно дадут суммарную характеристику с крутым наклоном, но «излом» этой амплитудно‑частотной характеристики не будет резким. Из многих плавных перегибов не сделать одного крутого.

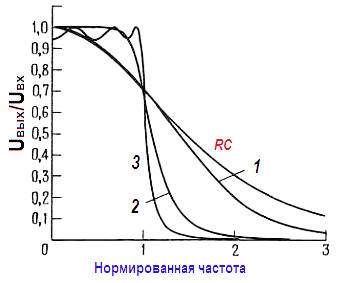
Чтобы проиллюстрировать этот вывод, построим несколько графиков частотных характеристик коэффициента усиления (т. е. U_вых/U_вх) фильтров нижних частот, составленных из 1, 2, 4, 8, 16 и 32 идентичных, полностью развязанных буферными усилителями RС‑звеньев.

На графике показан эффект от каскадного соединения нескольких RC‑звеньев, у каждого из которых точка, соответствующая значению –3 дБ, находится на единичной частоте.

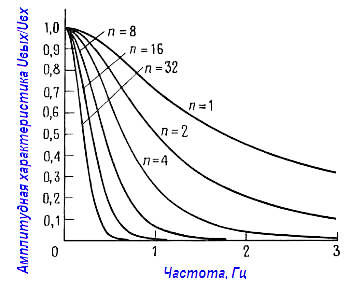
По мере добавления новых секций точка –3 дБ суммарной характеристики сдвигается в сторону низких частот, что легко было предсказать. Чтобы сравнение характеристик фильтров было корректным, надо таким образом согласовать частоты среза отдельных звеньев, чтобы частота, отвечающая значению –3 дБ, была одна и та же для сравниваемых фильтров.

Графики на рисунках ниже «нормированы» по частоте, в том смысле, что точка, отвечающая значению – 3 дБ (или точка перегиба), находится на частоте 1 рад/с (или 1 Гц).

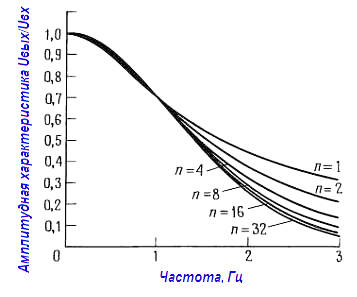
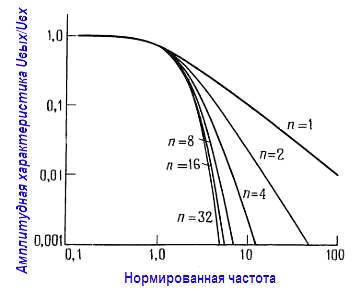
Для того чтобы определить характеристику фильтра, у которого точка перегиба находится на другой частоте, нужно просто изменить масштаб по оси частот с помощью умножения значений на частотной оси на истинное значение точки перегиба f_с. В данном случае (каскадное соединение RС‑звеньев) нормализованные графики демонстрируют плавный изгиб характеристики пассивных RС‑фильтров.

LC фильтр. Идеальный рабочий режим

Фильтры, построенные из конденсаторов и катушек индуктивности, могут иметь весьма крутые характеристики. Примером этого может служить параллельный резонансный LC‑контур. Введение в конструкцию катушек индуктивности дает возможность создать фильтр с любой желаемой близостью участка характеристики в полосе пропускания к горизонтальной прямой в сочетании с резкостью переходной области и крутизной спада вне полосы пропускания. На рисунках приведены в качестве примера телефонный фильтр и соответствующая характеристика.

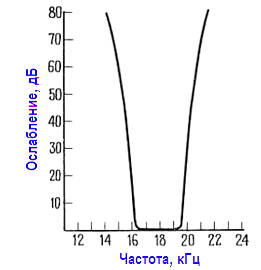
Очевидно, что введение катушек индуктивности в схему дает некий магический эффект, который без них не может быть достигнут. По терминологии теории цепей, эта магия заключается в наличии «внеосевых полюсов». Тем не менее, сложность фильтра возрастает по мере ужесточения требований к горизонтальности и плавности амплитудно‑частотной характеристики в полосе пропускания и к крутизне спада вне ее, приводя к увеличению числа элементов по сравнению с предыдущим фильтром. Переходная и фазочастотная характеристики, вообще говоря, также ухудшаются по мере приближения амплитудно‑частотной характеристики к идеальной прямоугольной форме (кирпичная стена).

Единственной проблемой является то, что катушки индуктивности как элемент схемы часто оставляют желать лучшего. Они нередко бывают дорогими и громоздкими, далеки от идеала, поскольку ведут к «потерям». Имеют значительное последовательное сопротивление, равно как и другие «патологии», такие, как нелинейность, распределенная межвитковая емкость обмотки и чувствительность к магнитным помехам. Следовательно, нужно найти способ построения фильтров без катушек индуктивности с характеристиками идеальных RLC-фильтров.

Основы активных фильтров

При использовании в качестве элемента схемы фильтра ОУ можно синтезировать характеристику любого RLC‑фильтра без применения катушек индуктивности. Такие безиндуктивные фильтры известны под названием «активные фильтры» из‑за наличия в их схеме активного элемента (усилителя).

Активные фильтры можно использовать для реализации фильтров нижних и верхних частот, полосовых и полосно‑подавляющих фильтров, выбирая тип фильтра в зависимости от наиболее важных свойств характеристики, таких, как максимальная равномерность усиления в полосе пропускания, крутизна переходной области или независимость времени запаздывания от частоты (далее об этом подробнее). Кроме того, можно построить как «всепропускающие фильтры» с плоской амплитудно‑частотной характеристикой, но нестандартной фазочастотной характеристикой (они также известны как «фазовые корректоры»), так и наоборот – фильтр с постоянным фазовым сдвигом, но с произвольной амплитудно‑частотной характеристикой.

Конвертеры отрицательного полного сопротивления и гираторы.

Есть два интересных схемных элемента, которые следует упомянуть в любом обзоре: это – конвертер отрицательного полного сопротивления (КОС) и гиратор. Эти устройства могут имитировать свойства катушек индуктивности, хотя в них кроме ОУ используются только конденсаторы и резисторы.

Раз это так, то можно делать безиндуктивные фильтры с идеальными свойствами RLС‑фильтра, таким образом – это по крайней мере один из способов реализации активных фильтров. КОС преобразует полное сопротивление в ему противоположное (т. е. с обратным знаком). Гиратор преобразует полное сопротивление в обратное (т. е. емкость в индуктивность).

КОС превращает конденсатор в «обратную» катушку индуктивности:

ZС = 1/jωC –> Zвх = j/ωC ,

т. е. в том смысле, что порождаемый ток запаздывает относительно приложенного напряжения, а его полное сопротивление имеет неправильную частотную зависимость (при возрастании частоты оно не растет, а убывает).

ZС = 1/jωC –> Zвх = jωCR2 ,

т. е. индуктивность которого L = CR2.

Существование гиратора делает интуитивно ясным тот факт, что можно построить безындуктивный фильтр, имитирующий любой фильтр, использующий катушки индуктивности: просто заменить каждую катушку «гиратированным» конденсатором. Такое применение гираторов вполне корректно, и ранее упомянутый телефонный фильтр построен именно таким способом. Кроме того, простая вставка гираторов в существующие RLC‑схемы позволяет создавать много иных структур фильтров.

Фильтры Саллена и Ки.

На рисунке приведен пример простого фильтра, построенного даже отчасти из интуитивных соображений.

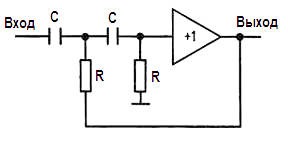
Он известен как фильтр Саллена и Ки, по имени его изобретателей. Здесь в качестве усилителя с единичным коэффициентом усиления может использоваться ОУ, включенный в режиме повторителя, либо просто эмиттерный повторитель.

Данный фильтр представляет собой двухполюсный фильтр верхних частот. Следует отметить, что это был бы просто двухкаскадный RС‑фильтр, если бы первый резистор не был соединен с выходом. Легко показать, что на очень низких частотах наклон характеристики такой же, как и у RС‑фильтра, поскольку выходной сигнал практически равен нулю. Рост же выходного сигнала при увеличении его частоты приводит к уменьшению ослабления в результате действия этой следящей связи, и за счет этого становится более резким излом характеристики.

Режимы работы фильтра

При анализе фильтров и при расчете их параметров всегда используются некоторые стандартные термины, и имеет смысл придерживаться их с самого начала. Частотная область. Наиболее очевидной характеристикой фильтра является зависимость его коэффициента передачи от частоты. Типичный случай – характеристика фильтра нижних частот, показанная на рисунках.

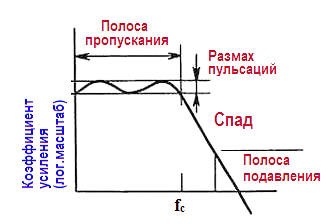
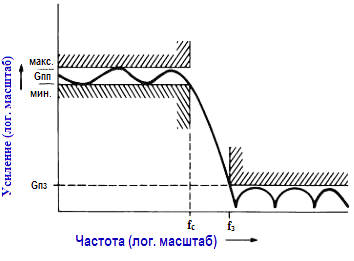
Здесь полоса пропускания представляет собой область частот, которые сравнительно мало ослабляются фильтром. Чаще всего считается, что полоса пропускания простирается до точки, соответствующей значению затухания – 3 дБ, но для некоторых фильтров (среди них замечательны фильтры с «равновеликими пульсациями») граница полосы пропускания может быть определена несколько иначе. Внутри же полосы пропускания характеристика может быть неравномерной, или пульсирующей, с определенным диапазоном (полосой) пульсаций характеристики, как это и показано на рисунке.

Частота среза f_с определяет границу полосы пропускания. Далее характеристика фильтра проходит через переходную область (известную также как «склон» характеристики фильтра) к полосе задерживания – области значительного ослабления. Полосу задерживания можно определить через некоторое минимальное затухание, например 40 дБ.

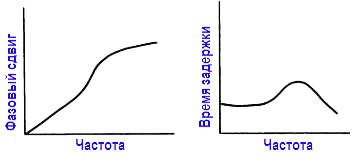
Наряду с характеристикой коэффициента передачи в частотной области важен и другой параметр, а именно сдвиг фазы выходного сигнала по отношению к входному. Другими словами, нас интересует комплексная частотная характеристика фильтра, которая обычно обозначается как H (s), где s = jω; s и Η – комплексные величины. Фазочастотная характеристика важна, поскольку сигнал, целиком расположенный по частоте в полосе пропускания, будет искажен, если время запаздывания при прохождении через фильтр не будет постоянным для различных частот.

Постоянство временной задержки (для всех частот) соответствует линейному возрастанию фазового сдвига в зависимости от частоты, поэтому термин фильтр с линейной фазочастотной характеристикой применяется к идеальному в этом отношении фильтру. На рисунке показаны типовые графики фазочастотной характеристики и амплитудно‑частотной характеристики фильтра нижних частот, который явно не является линейно‑фазовым фильтром.

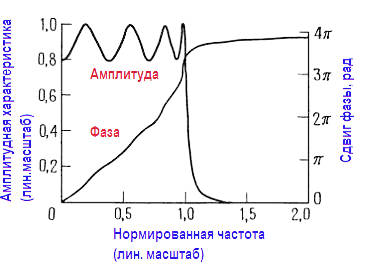
Графики фазочастотной характеристики лучше всего строить в линейном по частоте масштабе.

Временная область. Свойства фильтров, как и любых других схем переменного тока, могут быть описаны также их параметрами во временнóй области, а именно временем нарастания, выбросом, пульсациями и временем установления. Эти свойства важны, в частности, там, где должны использоваться ступенчатые или импульсные сигналы. На рисунке показана типичная переходная характеристика фильтра нижних частот.

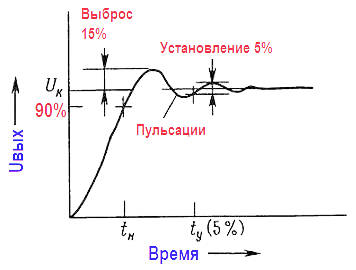
Здесь время нарастания представляет собой время, необходимое для достижения сигналом 90 % своего конечного значения, в то время как время установления – это время, необходимое для того, чтобы сигнал попал в некоторую окрестность конечного значения и там остался. Выброс и колебания описывают нежелательные свойства фильтра, смысл которых ясен из их названия.

Типы фильтров

Предположим, что требуется фильтр нижних частот с плоской характеристикой в полосе пропускания и резким переходом к полосе подавления. Окончательный же наклон характеристики в полосе задерживания всегда будет 6n дБ/октава, где n – число «полюсов». На каждый полюс необходим один конденсатор (или катушка индуктивности), поэтому требования к окончательной скорости спада частотной характеристики фильтра, грубо говоря, определяют его сложность.

Теперь предположим, что вы решили использовать 6 полюсный фильтр нижних частот. Вам гарантирован окончательный спад характеристики на высоких частотах 36 дБ/октава. В свою очередь теперь можно оптимизировать схему фильтра, за счет уменьшения крутизны перехода от полосы пропускания к полосе задерживания. С другой стороны, допуская некоторую неравномерность характеристики в полосе пропускания, можно добиться более крутого перехода от полосы пропускания к полосе задерживания. Третий критерий, который может оказаться важным, описывает способность фильтра пропускать сигналы со спектром, лежащим в полосе пропускания, без искажений их формы, вызываемых фазовыми сдвигами. Можно также интересоваться временем нарастания, выбросом и временем установления.

Известны методы проектирования фильтров, пригодные для оптимизации любой из этих характеристик или их комбинаций. Действительно разумный выбор фильтра происходит не так, как описано выше. Как правило, сначала задаются требуемая равномерность характеристики в полосе пропускания и необходимое затухание на некоторой частоте вне полосы пропускания и другие параметры. После этого выбирается наиболее подходящая схема с количеством полюсов, достаточным для того, чтобы удовлетворялись все эти требования.

Фильтры Баттерворта и Чебышева

Фильтр Баттерворта обеспечивает наиболее плоскую характеристику в полосе пропускания, что достигается ценой плавности характеристики в переходной области, т. е. между полосами пропускания и задерживания. Как будет показано дальше, у него также плохая фазочастотная характеристика. Его амплитудно‑частотная характеристика задается следующей формулой:

U_вых /U_вх = 1/[1 + (f /f_c )²ⁿ]^1/2

где n определяет порядок фильтра (число полюсов). Увеличение числа полюсов дает возможность сделать более плоским участок характеристики в полосе пропускания и увеличить крутизну спада от полосы пропускания к полосе подавления, как это показано на рисунке.

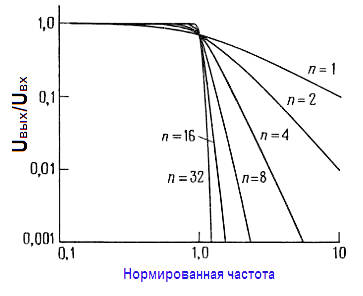
Выбирая фильтр Баттерворта, ради максимально плоской характеристики поступаемся всем остальным. Его характеристика идет горизонтально, начиная от нулевой частоты, перегиб ее начинается на частоте среза f _c ‑ эта частота обычно соответствует точке –3 дБ.

В большинстве применений самым существенным обстоятельством является то, что неравномерность характеристики в полосе пропускания не должна превышать некоторой определенной величины, скажем 1 дБ. Фильтр Чебышева отвечает этому требованию, при этом допускается некоторая неравномерность характеристики во всей полосе пропускания, но при этом сильно увеличивается острота ее излома. Для фильтра Чебышева задают число полюсов и неравномерность в полосе пропускания. Допуская увеличение неравномерности в полосе пропускания, получаем более острый излом.

Амплитудно‑частотная характеристика этого фильтра задается следующим соотношением:

U_вых /U_вх = 1/[1 + ε²C_n ²(f /f_c )]^1/2

где C_n ‑ полином Чебышева первого рода степени n , а ε – константа, определяющая неравномерность характеристики в полосе пропускания. Фильтр Чебышева, как и фильтр Баттерворта имеет фазочастотные характеристики, далекие от идеальных. На следующих рисунках представлены для сравнения характеристики 6‑полюсных фильтров нижних частот Чебышева и Баттерворта.

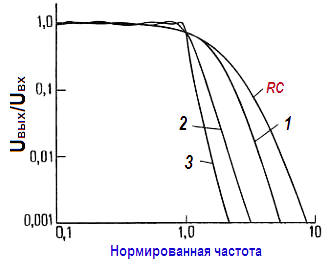
Как легко заметить, и тот, и другой намного лучше 6‑полюсного RC‑фильтра. На самом деле фильтр Баттерворта с максимально плоской характеристикой в полосе пропускания не столь привлекателен, как это может показаться, поскольку в любом случае приходится мириться с некоторой неравномерностью в полосе пропускания. Для фильтра Баттерворта это будет постепенное понижение характеристики при приближении к частоте f_с, а для фильтра Чебышева – пульсации, распределенные по всей полосе пропускания).

Кроме того, активные фильтры, построенные из элементов, номиналы которых имеют некоторый допуск, будут обладать характеристикой, отличающейся от расчетной. Это значит, что в действительности на характеристике фильтра Баттерворта всегда будет иметь место некоторая неравномерность в полосе пропускания. На рисунке проиллюстрировано влияние наиболее нежелательных отклонений значений емкости конденсатора и сопротивления, резистора на характеристику фильтра.

В свете вышеизложенного весьма рациональной структурой является фильтр Чебышева. Иногда его называют равноволновым фильтром, так как его характеристика в области перехода имеет большую крутизну за счет того, что по полосе пропускания распределено несколько равновеликих пульсаций, число которых возрастает вместе с порядком фильтра. Даже при сравнительно малых пульсациях (порядка 0,1 дБ) фильтр Чебышева обеспечивает намного большую крутизну характеристики в переходной области, чем фильтр Баттерворта. Чтобы выразить эту разницу количественно, предположим, что требуется фильтр с неравномерностью характеристики в полосе пропускания не более 0,1 дБ и затуханием 20 дБ на частоте, отличающейся на 25 % от граничной частоты полосы пропускания. Расчет показывает, что в этом случае требуется 19‑полюсный фильтр Баттерворта или всего лишь 8‑полюсный фильтр Чебышева.

Мысль о том, что можно мириться с пульсациями характеристики в полосе пропускания ради увеличения крутизны переходного участка, доводится до своего логического завершения в идее так называемого эллиптического фильтра (или фильтра Кауэра), в котором допускаются пульсации характеристики как в полосе пропускания, так и в полосе задерживания ради обеспечения крутизны переходного участка даже большей, чем у характеристики фильтра Чебышева. С помощью ЭВМ можно сконструировать эллиптические фильтры так же просто, как и классические фильтры Чебышева и Баттерворта.

На следующем рисунке представлено графическое задание амплитудно‑частотной характеристики фильтра.

В этом случае (фильтр нижних частот) определяются допустимый диапазон коэффициента передачи фильтра (т. е. неравномерность) в полосе пропускания, минимальная частота, на которой характеристика покидает полосу пропускания, максимальная частота, где характеристика переходит в полосу задерживания, и минимальное затухание в полосе задерживания.

Фильтры Бесселя

Как было установлено ранее, амплитудно‑частотная характеристика фильтра не дает о нем полной информации. Фильтр с плоской амплитудно‑частотной характеристикой может иметь большие сдвиги фаз. В результате этого форма сигнала, спектр которого лежит в полосе пропускания, будет искажена при прохождении через фильтр. В ситуации, при которой форма сигнала имеет первостепенное значение, желательно иметь в распоряжении линейно‑фазовый фильтр (фильтр с постоянным временем запаздывания). Предъявление к фильтру требования обеспечения линейного изменения сдвига фазы в зависимости от частоты равносильно требованию постоянства времени запаздывания для сигнала, спектр которого расположен в полосе пропускания, т. е. отсутствия искажений формы сигнала.

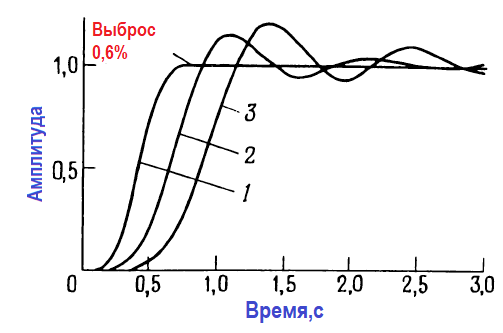
Фильтр Бесселя (также называемый фильтром Томсона) имеет наиболее плоский участок кривой времени запаздывания в полосе пропускания, подобно тому, как фильтр Баттерворта имеет наиболее плоскую амплитудно‑частотную характеристику. Чтобы понять, какое улучшение во временной области дает фильтр Бесселя, посмотрите на рисунок ниже, где изображены нормированные по частоте графики времени запаздывания для 6‑полюсных фильтров нижних частот Бесселя и Баттерворта.

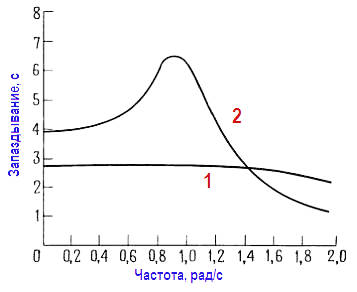
Плохая характеристика времени запаздывания фильтра Баттерворта обуславливает появление эффектов типа выброса при прохождении через фильтр импульсных сигналов. С другой же стороны, за постоянство времен запаздывания у фильтра Бесселя приходится расплачиваться тем, что его амплитудно‑частотная характеристика имеет еще более пологий переходной участок между полосами пропускания и задерживания, чем даже у характеристики фильтра Баттерворта.

Существует много различных способов проектирования фильтров, в которых делаются попытки улучшить рабочие параметры фильтра Бесселя во временной области. При этом частично жертвуя постоянством времени запаздывания ради уменьшения времени нарастания и улучшения амплитудно‑частотной характеристики. Фильтр Гаусса имеет почти столь же хорошие фазочастотные характеристики, как и фильтр Бесселя, но при улучшенной переходной характеристике.

Другой интересный класс представляют собой фильтры, позволяющие добиться одинаковых по величине пульсаций кривой времени запаздывания в полосе пропускания (аналогично пульсациям амплитудно‑частотной характеристики фильтра Чебышева) и обеспечивающие примерно одинаковое запаздывание для сигналов со спектром вплоть до полосы задерживания. Еще один подход к созданию фильтров с постоянным временем запаздывания – это применение всепропускающих фильтров, называемых иначе корректорами во временной области. Эти фильтры обладают постоянной амплитудно‑частотной характеристикой, а сдвиг фазы может меняться согласно конкретным требованиям. Таким образом, их можно применять для выравнивания времени запаздывания любых фильтров, в частности фильтров Баттерворта и Чебышева.

Сравнение фильтров

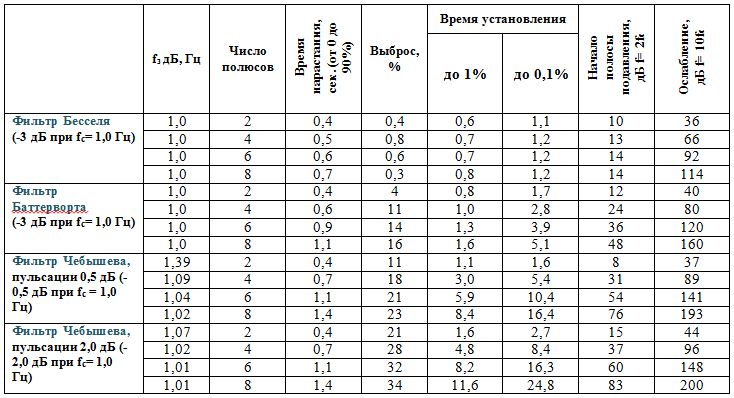
Несмотря на ранее высказанные замечания о переходной характеристике фильтров Бесселя, он все же обладает очень хорошими свойствами во временной области по сравнению с фильтрами Баттерворта и Чебышева. Сам фильтр Чебышева при его весьма подходящей амплитудно‑частотной характеристике имеет наихудшие параметры во временной области из всех этих трех типов фильтров. Фильтр Баттерворта дает компромисс между частотами и временными характеристиками.

В таблице и на рисунке ниже дана информация по рабочим характеристикам этих трех типов фильтров во временной области, дополняющая приведенные ранее графики амплитудно‑частотных характеристик. По этим данным можно сделать вывод, что в тех случаях, когда важны параметры фильтра во временной области, желательно применять фильтр Бесселя.