Псевдослучайные битовые последовательности и генераторы шума
Интересная смесь цифрового и аналогового подходов обнаруживается в теме псевдослучайных битовых последовательностей – ПСДП или PRBS. Оказывается, создавать последовательности битов или слов с хорошей степенью случайности достаточно легко. Речь идёт о последовательностях с определёнными вероятностными и корреляционными свойствами как в идеальном автомате для подбрасывания монеты. Из-за того, что указанная задача выполняется стандартным предсказуемым логическим элементом — сдвиговым регистром, результат получается предсказуемым и повторяемым, хотя для стороннего наблюдателя любая часть такой последовательности выглядит как случайный набор нулей и единиц.

Цифровая генерация шума
Всего несколько микросхем позволяют создавать последовательности, которые будут тянуться без повторений веками. Таким образом, имеем удобный и привлекательный метод получения аналогового шума. При проверке уровня ошибок (BER) в последовательных каналах и получении «глазковых» диаграмм обычно используют PRBS.
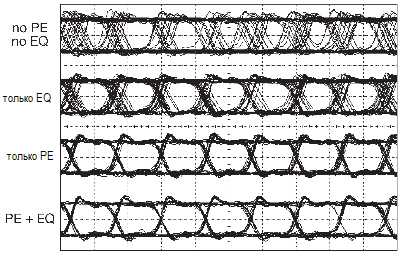
Такие же генераторы используются при предсказуемом кодировании (или скремблировании от «scramble») последовательных данных в гигабитных Ethernet каналах. Это нужно для получения переменного сигнала для трансформаторных развязок в физическом канале. На приёмной стороне та же синхронная псевдослучайная последовательность удаляется с помощью операции XOR, которая восстанавливает исходные данные.
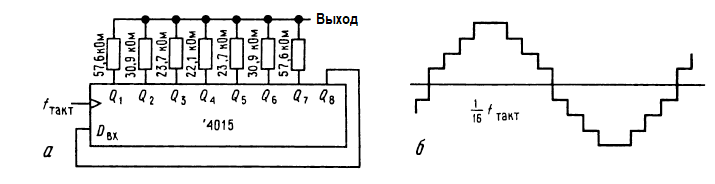
Аналоговый шум. С помощью простого ФНЧ из PRBS можно создать белый шум с гауссовым распределением, ограниченный по полосе, т.е. вплоть до определённой частоты шумовое напряжение будет иметь плоский спектр мощности. Тот же результат можно получить, суммируя данные на отдельных разрядах сдвигового регистра с индивидуальными весовыми коэффициентами (с помощью резисторов разных номиналов), т.е. проводя цифровую фильтрацию. Таким образом, легко можно получить шум с плоским спектром и верхней рабочей частотой до нескольких мегагерц. Как будет ясно из дальнейшего, цифровые источники шума имеют много преимуществ перед чисто аналоговыми методами — диодами и резисторами.
Другие приложения. Помимо очевидного использования в качестве источников аналогового шума псевдослучайные последовательности используются в приложениях, не имеющих ничего общего с шумом. К ним относятся тестовые последовательности для проверки последовательных линий связи (глазковые диаграммы, проверка на ошибки в канале) и для скремблирования (как замену шифрованию) в сетевых протоколах типа Ethernet. Они используются в широкополосных схемах связи с подавлением несущей, где каждый быт передаётся в виде определённого сочетания коротких пачек кодированных импульсов. Такой метод используется в сотовой связи стандарта CDMA, системе кодирования сигнала в GSM и при передаче цифрового телесигнала. Такие последовательности используются в проверочных и корректирующих кодах, потому что они позволяют такое преобразование блоков данных, при котором корректные данные разделяет наибольшая «дистанция Хемминга» (измеряемая числом однобитовых ошибок).
[* проще говоря, сколько битовых ошибок надо наложить на правильно закодированный элемент данных, чтобы он превратился в другой правильный элемент, т.е. элемент, который система примет в качестве правильного, но который на самом деле есть результат деструктивного воздействия серии ошибок. Для обычной системы контроля чётности дистанция Хемминга равна двум.]
Автокорректирующий характер псевдослучайных кодов определяет удобство модуляции ими радарных сигналов. Принимаемый эхо-сигнал сравнивается (точнее проходит процесс кросс-корреляции) с переданной последовательностью. Наконец, такие коды можно использовать в делителях «по-модулю-n».
Битовые последовательности на сдвиговых регистрах с обратными связями
Самые простые и популярные генераторы псевдослучайных последовательностей делаются на сдвиговых регистрах с линейными обратным связями (LFSR).
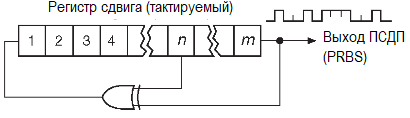
Сдвиговый регистр длины m бит тактируется некоторой частотой f0. Элемент «ИСКЛЮЧАЮЩЕЕ-ИЛИ» проводит одноимённую операцию (сложение «по-модулю-2») над промежуточным n-ным и выходным m-ным битами, а результат подаёт на вход регистра. Такая схема проходит через последовательность состояний, которая определяется длиной регистра и повторяется через K тактов.
Максимальное число возможных состояний m-разрядного регистра K=2m , т.е. число возможных сочетаний m чисел с двумя возможными значениями. К сожалению, состояние «все нули» зацикливается такой схемой, потому что «ИСКЛЮЧАЮЩЕЕ-ИЛИ» воспроизводит «0» на входе регистра. Таким образом, максимальная длина битовой последовательности такой схемы 2m-1. Очевидно, что такой результат можно получить, если m и n выбраны корректно, и итоговая последовательность и в самом деле псевдослучайная. В качестве примере рассмотрим 4-разрядный регистр с обратной связью.
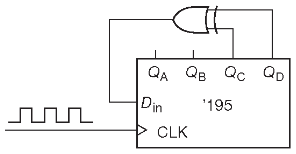
Пусть он начинает работу с состояния 1111 (оно может быть любым, кроме 0000), тогда имеет место следующая последовательность:
1111 → 0111 → 0011 → 0001 → 1000 → 0100 → 0010 → 1001 →
→ 1100 → 0110 → 1011 → 0101 → 1010 → 1101 → 1110
Состояния регистра записаны в формате QAQBQCQD. Схема имеет 15 различных состояний (24–1), после прохождения которых цикл повторяется. Следовательно, данный регистр является регистром максимальной длины.
Отводы для обратной связи. Сдвиговые регистры максимальной длины можно выполнить с числом отводов в цепи обратной связи больше 2 (в этом случае используются несколько вентилей ИСКЛЮЧАЮЩЕЕ ИЛИ, соединенных в виде стандартного дерева четности, т. е. в виде суммы по модулю 2 нескольких разрядов). На самом деле, для некоторых значений m регистр максимальной длины можно сделать только в том случае, когда число отводов будет больше 2. Ниже перечислены все значения m до 40, для которых регистр максимальной длины реализуется с использованием ровно двух отводов, т. е. с обратной связью от n-го и m-го (последнего) разрядов по типу регистра, приведенного ранее. Представлены также значения n и длина цикла К по числу тактов. В некоторых случаях подойдут и другие значения n и во всех случаях n можно заменить на m – n. Таким образом, для предыдущего примера можно использовать отводы n = 1 и m = 4.

Стандартные сдвиговые регистры имеют длину, кратную 8 (и 4), и если есть желание использовать все разряды, то придётся складывать более двух битов. В этих случаях может потребоваться более двух отводов. Вот эти магические числа:
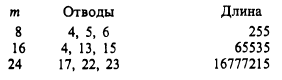
Регистры с длиной большей 32 бит требуются редко: при частоте тактирования 1 MHz время повторения последовательности около часа. Для длины 64 бита и частоты 1 GHz на второй круг она пойдёт через шестьсот лет.
Свойства последовательностей максимальной длины на сдвиговых регистрах с обратными связями. Очередной псевдослучайный бит создаётся в регистре с приходом активного фронта тактового сигнала и выдвигается наружу вслед за предыдущими элементами последовательности. Брать его можно из любого разряда регистра, но обычно используют последний (m-ный). Последовательности максимальной длины на сдвиговых регистрах обладают следующими свойствами:
В каждом полном цикле из K тактов число единиц на одну больше числа нулей. Дополнительная единица появляется из-за исключения состояния «все нули». Это значит, что появление и единицы, и нуля равновероятно (дополнительная единица совершенно незаметна на фоне общего числа состояний сколь-нибудь длинного регистра: один цикл 17-разрядного регистра состоит из 65536 единиц и 65535 нулей).
В одном полном цикле (K тактов) половина общего числа фрагментов из одних единиц имеет длину 1, четверть — длину 2, одна восьмая — длину 3 и т.д. Число фрагментов, состоящих из одних нулей, равно числу фрагментов из одних единиц такой же дины, исключая один пропущенный нуль. Это означает, что вероятность появления нуля или единицы не зависит от значения предыдущего бита, т.е. вероятность завершения фрагмента из одинаковых цифр равна 1/2.
Если одна последовательность полной длины (K тактов) сравнивается с тем же набором нулей и единиц, циклически сдвинутым на какое-либо число тактов n (где n не равно 0 и не кратно K), число несовпадений будет на единицу больше числа совпадений. Или та же мысль в строгой форме: автокоррелирующая функция является дельтой Кронера при нулевой задержке и –1/K во всех остальных случаях. Отсутствие боковых «лепестков» автокоррелирующих функций делает их очень удобными для использования в радарах.
Генерация аналогового шума с помощью последовательностей максимальной длины
Преимущества цифровой генерации шума. Как отмечалось ранее, цифровой выходной сигнал сдвигового регистра с обратными связями можно превратить в белый шум с ограниченной полосой с помощью ФНЧ с частотой среза, лежащей гораздо ниже тактовой частоты. До погружения в технические подробности отметим некоторые преимущества цифровой генерации аналогового шума. Среди прочего такой способ позволяет создавать шум с известным спектром и амплитудой и вдобавок с изменяемой рабочей полосой (которая прямо зависит от тактовой частоты) на простом надёжном цифровом устройстве. У данного метода нет проблем с разбросом параметров как в генераторах на шумовых диодах, нет наводок на чувствительную слаботочную схему на резисторе или диоде. Наконец, жёсткая заданность последовательности позволяет получить с помощью взвешенного цифрового фильтра повторяемую, независимую от тактовой частоты (т.е. рабочей полосы) форму шумового сигнала.
Спектр мощности последовательностей на сдвиговых регистрах. Выходной спектр, создаваемый сдвиговым регистром, состоит из шума начинающегося с частоты повторения полной последовательности fclk/K и уходит выше частоты тактирования fclk. Он ровный в пределах ±0.1 dB до частоты 0.12fclk и начинает довольно быстро падать выше точки «-3dB» (0.44 fclk). Таким образом, ФНЧ с частотой среза на уровне 5…10% тактовой частоты превратит выходной сигнал со сдвигового регистра в аналоговый шум с ограниченной полосой. Достаточно простого RC фильтра, но если нужны очень точные границы, то могут потребоваться активные фильтры с крутыми срезами.
Рассмотрим выходной сигнал сдвигового регистра и его спектр мощности. В обычной ситуации постоянные смещения нежелательны, поэтому для «0» берётся напряжение –a, а для «1» +a.
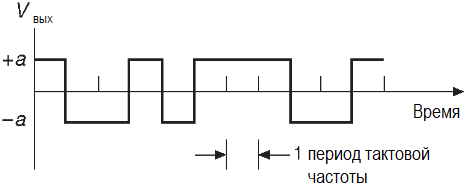
Делать это можно разными способами, некоторые из которых показаны на рисунке.
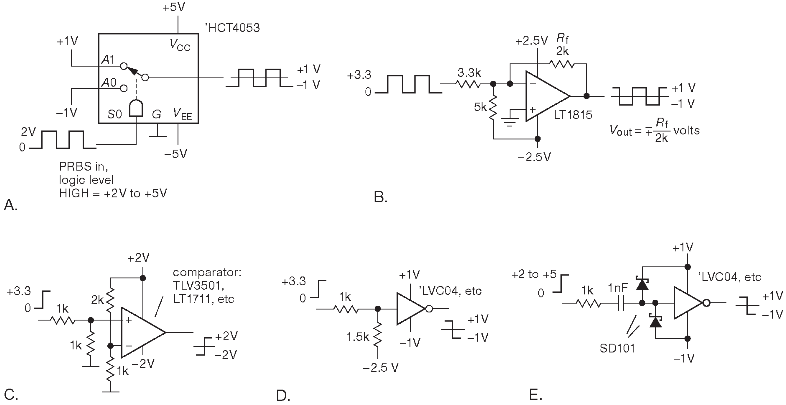
- С помощью аналогового КМОП ключа ‘HC4053, работающего с двумя питаниями и потенциалам +a и –a на входах.
- С помощью быстрого ОУ с компенсацией тока постоянного смещения в суммирующей точке.
- С помощью быстрого компаратора, работающего от разделённого источника ±a вольт.
- С помощью КМОП логического элемента, питающегося от источников ±a вольт с делителем на входе.
- Тот же логический элемент, включённый по переменному току с диодным ограничителем.
Варианты с логическим элементом несколько переусложнены и допустимы, только если общее питание (V =2a) попадает в диапазон питания стандартных логических семейств (1…5 V). Зато тут всё хорошо со скоростью переключения. Последний вариант не имеет связи по постоянному току и требует, чтобы логический вход постоянно находился в каком-либо корректном состоянии, но здесь данное условие выполняется: PRBS не может замереть дольше, чем на m тактов 137.
Как уже говорилось ранее, цепочка выходных битов имеет единственный пик автокорреляционной функции. График цифровой дискретной автокорреляционной функции (сумма произведений соответствующих битов, когда последовательность сравнивается со своей сдвинутой копией и имеет на выходе только +1 и –1), показан на рисунке.
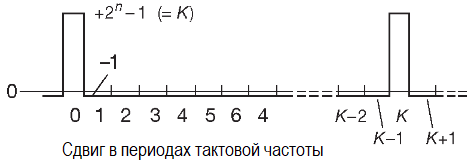
Её не следует путать с непрерывной автокорреляционной функцией, которая будет рассмотрена позднее. Приведённый график определён только для сдвигов на целое число тактов. Для всех тактов, чей номер не кратен периоду повторения K, автокорреляционная функция имеет постоянное значение –1 (потому что в последовательности есть лишняя единица). Это смещение совершенно незначительно по сравнению с величиной K у функции без смещения. Аналогично, если рассматривать неотфильтрованный выход сдвигового регистра как аналоговый сигнал (имеющий только два значения +a и –a),
[* и теперь непрерывный во времени: цифровой сигнал имеет разрывы графика на каждом фронте — вертикальных соединений там нет]
нормализованная автокорреляционная функция станет непрерывной, и её график будет соответствовать рисунку:
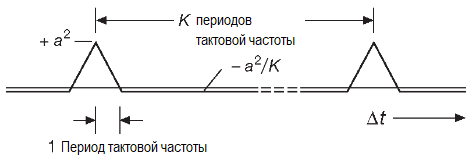
Другими словами, сигнал совершенно не коррелирован (не совпадает) сам с собой при сдвиге копии на ненулевое (но не кратное K) число тактов вперёд или назад.
Спектр мощности неотфильтрованного цифрового выхода можно получить из коэффициента автокорреляции с помощью стандартных математических методов. Результатом будет серия равномерно расположенных пачек пиков (дельта-функций), которые повторяются через промежутки fclock/K (на рисунке ниже они обозначены «всплески разделены интервалами…»), начиная с частоты повторения полной последовательности fclock/K.
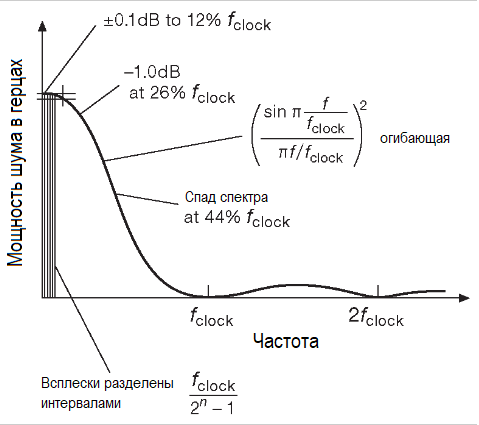
Линейчатый характер спектра отражает тот факт, что последовательность с течением времени повторяет саму себя. Пугаться не надо: спектр будет непрерывным для любого измерения, продолжающегося меньше, чем длительность одного периода повторения псевдослучайной последовательности. Огибающая нефильтрованной цифровой последовательности (волновой конверт) соответствует квадрату функции sinx/x. Отметим присущую ей особенность — отсутствие мощности шума на частоте тактирования и её гармониках.
Напряжение шума. При генерации аналогового шума используется, разумеется, только часть низкочастотной области спектра. Оказывается, что удельную мощность шума на герц несложно выразить через половинную амплитуду а и тактовую частоту fтакт. Мощность, выраженная через среднеквадратичное напряжение шума, будет иметь вид:
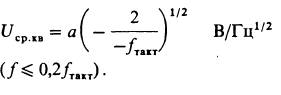
Это относится к нижней части спектра, т. е. к той части, которая обычно используется (для того, чтобы определить плотность мощности в любой части спектра, можно использовать огибающую).
Предположим, например, что регистр сдвига максимальной длины работает на частоте 1,0 МГц и организован таким образом, что выходное напряжение изменяется от +10,0 до -10,0 В. Выходной сигнал пропускается через RC- фильтр нижних частот с затуханием 3 дБ на частоте 1 кГц
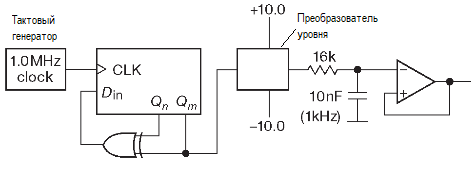
Можно точно вычислить среднеквадратичное напряжение шума на выходе. Из предыдущего выражения мы знаем, что среднеквадратичное напряжение на выходе преобразователя уровней равно 14,14 мВ/Гц1/2. Мы знаем также, что полоса шума НЧ-фильтра составляет (π/2) (1,0 кГц) или 1,57 кГц. Поэтому выходное напряжение шума будет равно Ucp.кв = 0,01414 • (1570)1/2 = 560 мВ, а его спектр будет соответствовать низкочастотному АС-фильтру.
Фильтрация по низким частотам
Аналоговая фильтрация. Полезный спектр шума, создаваемого генератором псевдослучайной последовательности, простирается от низкочастотной границы, обратной периоду повторения (fтакт/К), до высокочастотной границы, равной примерно 20% от тактовой частоты (на этой частоте мощность шума на герц падает на 0,6 дБ). Простая низкочастотная фильтрация с использованием RС-звеньев, как показано в предыдущем примере, равнозначна установке точки 3 дБ намного ниже тактовой частоты (например, ниже 1% fтакт). Для того чтобы использовать часть спектра более близкую к тактовой частоте, желательно применить фильтры с более крутым срезом, например фильтры Баттерворта или Чебышева. В этом случае плоскость результирующего спектра будет определяться параметрами фильтра, которые должны быть измерены, поскольку отклонения в параметрах могут вызывать колебания коэффициента передачи в полосе пропускания. С другой стороны, если требуется точное значение напряжения шума на Гц-1/2, то необходимо измерить реальный коэффициент передачи фильтра по напряжению.
Цифровая фильтрация. Недостаток аналоговой фильтрации заключается в том, что если тактовая частота изменяется в несколько раз, то требуется подстройка частоты среза фильтра. В тех случаях, где это необходимо, изящное решение дает цифровая фильтрация, которая осуществляется с помощью взвешенной аналоговой суммы последовательных выходных разрядов (нерекурсивная цифровая фильтрация). С ее помощью эффективная частота среза подстраивается под изменение тактовой частоты. Кроме того, цифровая фильтрация позволяет спуститься до предельно низких частот среза (доли герца), где аналоговая фильтрация становится практически беспомощной.
Для того чтобы осуществить взвешенное суммирование одновременно нескольких последовательных выходных разрядов, можно просто воспользоваться различными параллельными выходами разрядов регистра сдвига и использовать резисторы различного номинала, подключенные к суммирующей точке операционного усилителя. Для НЧ-фильтра весовые коэффициенты должны быть пропорциональны (sinx)/x. Обратите внимание, поскольку весовые коэффициенты могут быть обоих знаков, потребуется инвертирование некоторых уровней. Так как в этой схеме не используются конденсаторы, выходной сигнал будет состоять из набора дискретных уровней выходного напряжения.
Приближение к гауссовому распределению улучшается по мере увеличения числа суммируемых разрядов. Дополнительным плюсом является сглаживание формы выходного сигнала. По этой причине желательно использовать столько разрядов сдвигового регистра, сколько возможно, добавляя нужное количество дополнительных секции регистра уже после линий обратных связей. Как и ранее, чтобы получить нужное входное напряжение, надо использовать подтягивающие резисторы или твердотельные ключи. Для такой задачи идеальна КМОП логика, имеющая в качестве рабочих уровней точные потенциалы земли и питания.
Устройство на рисунке ниже построено по описанной схеме и создаёт псевдослучайный аналоговый шум с полосой, которая меняется в очень широких пределах.
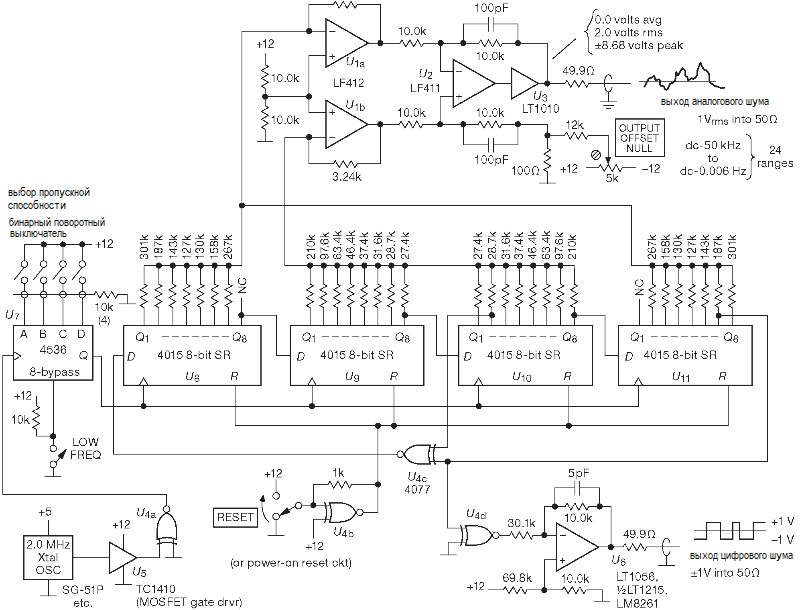
Сигнал с генератора 2.0 MHz идёт на 24-разрядный программируемый делитель ’14536, на выходе которого получается набор частот от 0.12 Hz до 1 MHz, соответствующих двоичным коэффициентам деления. Сдвиговый регистр длиной 32 бита включён с отводами от 31 и 18 разрядов и создаёт последовательность максимальной длины с двумя миллиардами состояний (полный цикл при максимальной тактовой частоте составляет один час). В примере используется взвешенное суммирование 32 последовательных значений функции (sin x)/x. Операционные усилители U1a и U1b масштабируют прямые и инверсные элементы суммы соответственно, а итоговый сигнал формируется на U2.
Усиление подобрано таким образом, чтобы получить сигнал без постоянной составляющей амплитудой 1.0Vrms на нагрузке 50 Ω (или 2.0Vrms без нагрузки). Отметим, что указанные напряжения не зависят от тактовой частоты, т.е. рабочей полосы. Частота среза цифрового фильтра составляет 0.05fclock, что позволяет получить белый шум в 24 диапазонах в полосе до 50 kHz (на максимальной частоте) и вплоть до 0.006 Hz (на минимальной). Схема имеет и нефильтрованный выход ±1V.
Схема имеет несколько интересных особенностей. В качестве элемента обратной связи используется вентиль «ИСКЛЮЧАЮЩЕЕ-ИЛИ» с инверсией, что позволяет инициализировать регистр простым сбросом. В таком включении выбрасывается недопустимая комбинация «все единицы», в отличии от обратной связи на обычном «ИСКЛЮЧАЮЩЕМ-ИЛИ», где недопустимы «все нули». Все остальные свойства псевдослучайной последовательности сохраняются.
Взвешенная сумма конечного числа элементов не может создать настоящее гауссово распределение шумовых амплитуд, потому что их максимальная величина ограничена (конечностью суммы). В данном примере расчёт даёт +4.34 V на нагрузке 50 Ω, т.е. пик-фактор равен 4.34. Это достаточно важная величина, потому что усиление U1 и U2 должно выбирать так, чтобы исключить ограничение в выходном каскаде. И, наконец, интересен метод получения выходного сигнала с нулевым синфазным напряжением из логических уровней КМОП (НИЗКИЙ = 0V, ВЫСОКИЙ = 12.0 V).
Краткое заключение
Несколько заключительных замечаний относительно последовательностей, генерируемых регистрами сдвига, как источников аналогового шума. На основании трех перечисленных ранее свойств регистров максимальной длины, возможно можно заключить, что выходная последовательность «чересчур случайна» в том смысле, что она имеет точное число серий заданной длины и т.п. Настоящая случайная машина для подбрасывания монеты не генерировала бы на единицу больше «орлов», чем «решек», а ее автокорреляционная функция не была бы абсолютно плоской для конечной последовательности. Посмотрите на это с другой стороны. Если бы мы использовали единицы и нули, вырабатываемые регистром сдвига, для управления случайным блужданием, двигаясь вперед на один шаг при получении единицы и назад на один шаг при получении нуля, то оказались бы на расстоянии ровно в один шаг от начальной точки после того, как регистр пройдет весь цикл. Этот результат уж никак нельзя назвать случайным!
Вместе с тем упомянутые свойства регистра сдвига верны только для всей последовательности из 2n — 1 бит, взятой как одно целое. Если вы используете фрагмент полной битовой последовательности, то его свойства будут довольно точно аппроксимировать случайный автомат для подбрасывания монеты. Представьте себе аналогичный процесс — извлечение красных и синих шаров наугад из урны, в которую вначале помещены К шаров (половина красных, половина синих). Если вы вытаскиваете шары без возвращения, то сначала вы рассчитываете получить почти случайную статистику. По мере убывания шаров в урне статистика изменяется за счет того, что общее число красных и синих шаров должно оставаться тем же самым.
Представление о том, как это происходит, можно получить, вновь вернувшись к случайному блужданию. Если предположить, что единственным «неслучайным» свойством последовательности является точное равенство «1» и «0» (не обращая внимание на одну лишнюю «1»), то можно показать, что описанное случайное блуждание после r вытаскиваний из общей «популяции» К/2 единиц и К/2 нулей приведет к среднему расстоянию от начальной точки, равному
X = [r(К — r)/(K — 1)]1/2.
(Этим выражением мы обязаны Е. М. Purcell.) Поскольку при полностью случайном блуждании X равно корню квадратному из r, коэффициент (К — r)/(К -1) отражает влияние конечных содержимых урны. Пока r<<К, случайность блуждания чуть-чуть отличается от случая абсолютно случайного блуждания, и генератор псевдослучайной последовательности практически неотличим от реального автомата. Проверив это на нескольких тысячах случайных блужданий под управлением ПСП (каждое в несколько тысяч шагов), обнаружим идеальную случайность по этому простому критерию.
Тот факт, что генераторы ПСП выдерживают этот тест, разумеется, не гарантирует, что они будут удовлетворять и более сложным тестам на случайность, например тестам на корреляцию более высокого порядка. Такие корреляционные зависимости также оказывают влияние на свойства аналогового шума, генерируемого путем фильтрации ПСП. Несмотря на то, что амплитуда шума имеет гауссово распределение, возможно наличие корреляции амплитуд более высокого порядка, не свойственной настоящему случайному шуму. По этому поводу сейчас принято считать, что чем больше отводов участвует в обратной связи (предпочтительно порядка m/2), тем «лучше» шумовые свойства (при использовании для формирования последовательных входов дерева четности на элементах ИСКЛЮЧАЮЩЕЕ ИЛИ).
Разработчикам генераторов шума следует познакомиться со сдвиговым регистром переменной длины ’4557. Он имеет шесть входов управляющих длиной, которые позволяют выставить любое значение от 1 до 64 шагов. ’4557 удобно использовать в связке с ’4015 или ’164, чтобы получить отвод в n-ной позиции. Другой удобной микросхемой является ’HC(T)7731 — счетверённый 64-разрядный сдвиговый регистр (всего 256 битов), который может работать на частоте до 30 MHz (min). Ещё удобнее и проще создавать PRBS с помощью программируемой логики. Задачу могут решать и микроконтроллеры, но PLD работают быстрее.
Если нужна очень высокая скорость, можно возвратиться к старой доброй дискретной логике, как это сделано в «программируемом тактовом генераторе» CG635 фирмы Stanford Research Systems, который может выдавать 7-шаговые PRBS (27–1) на частоте 1.55 GHz. Делается это с использованием некоторых изящных трюков.
- В качестве кучи триггеров взяты представители дифференциальной эмиттерно-связанной логики MC100EP52D. Это быстрый D-триггер имеет время установки 0.05 ns, нулевое время удержания и 0.33 ns (тип.) время распространения.
- Они используют тихие и быстрые дифференциальные линии данных и тактовый сигнал.
- Узкое место — время распространения в элементе «ИСКЛЮЧАЮЩЕЕ-ИЛИ» — 0.3 ns, поэтому
- цепочка триггеров закольцована, причём линия данных идёт по часовой стрелке, а линия тактирования — против часовой. Такое включение даёт для первого триггера задержку тактового сигнала относительно двух последних порядка 0.25 ns, что позволяет учесть время установки данных от элемента «ИСКЛЮЧАЮЩЕЕ-ИЛИ».
Описанная геометрия платы вызывает задержку тактового сигнала между триггерами порядка 0.05 ns, позволяя красиво решить непростую задачу разводки тактового сигнала.
Цифровые фильтры
Последний пример затронул интересную тему цифровой фильтрации, в данном случае формирование НЧ-сигнала путем взвешенного суммирования 32 значений псевдослучайной последовательности, каждое из которых соответствует уровню напряжения 0 или +12 В. На вход такого «фильтра» поступают сигналы, которые могут иметь только два уровня напряжения. Вообще говоря, то же самое можно сделать с аналоговым сигналом на входе, образуя взвешенную сумму его значений (xi), распределенных во времени через равные интервалы
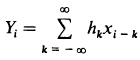
Здесь xi являются дискретными выборками из входного сигнала, hk—весовые коэффициенты, а yi — значения выходного сигнала. В реальных условиях цифровой фильтр будет суммировать только конечное множество входных значений, как, например, в генераторе шума, где было использовано 32 члена. На рисунке схематично показано, как это происходит.
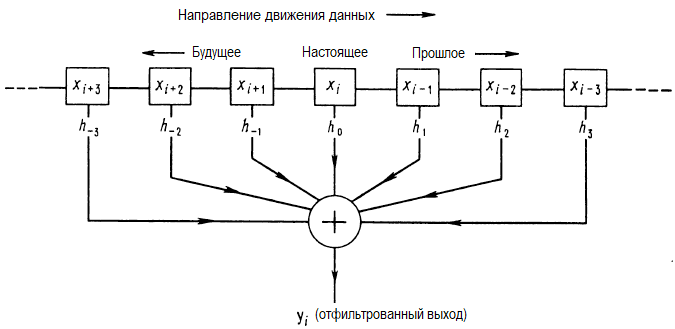
Заметьте, что такой фильтр может обладать интересным свойством симметричности во времени, т. е. усреднением прошлого и будущего для того, чтобы сформировать текущее значение выхода.
Разумеется, реальные аналоговые фильтры умеют лишь смотреть в прошлое и соответствуют цифровым фильтрам с ненулевыми весовыми коэффициентами только при k ≥ 0.
Частотная характеристика симметричного фильтра. Можно показать, что частотная характеристика симметричного фильтра (hk = h—k) имеет вид

где tотс-время между выборками (отсчетами). Нетрудно заметить, что hk представляют собой коэффициенты разложения в ряд Фурье требуемой частотной характеристики. Это объясняет, почему в случае представленной ранее схемы генератора весовые коэффициенты были выбраны в соответствии с функцией (sin х)/х: они являются компонентами Фурье заграждающего НЧ-фильтра. В таких симметричных фильтрах фазовый сдвиг на любой частоте либо равен 0, либо 180°.
Рекурсивные фильтры. Можно получить интересный класс цифровых фильтров, если на вход фильтра в дополнение к внешнему входному сигналу подать собственный выходной сигнал фильтра. Такой фильтр можно рассматривать как фильтр с обратной связью. Он имеет причудливое название рекурсивный фильтр (или с бесконечной импульсной характеристикой) в противоположность рассмотренному выше не рекурсивному (с конечной импульсной характеристикой) фильтру. Можно, например, сформировать выходной сигнал в соответствии со следующим выражением:
yi = Ayi -1 + (1 — A)xi
Это соответствует низкочастотной характеристике, эквивалентной той, которой обладает простой низкочастотный RС- фильтр
А = е —tотс/RC
где tотс — интервал времени между последовательными выборками Xi из входного сигнала. Эта ситуация, конечно, не является идентичной ситуации с аналоговым низкочастотным фильтром, работающим с аналоговым сигналом, по причине дискретной природы отсчетов.
Пример НЧ-фильтра. В качестве числового примера предположим, что вам требуется отфильтровать ряд числовых значений, соответствующих сигналу с затуханием 3 дБ на частоте f3дБ = 1/20tотс. Таким образом, постоянная времени соответствует интервалу времени 20 последовательных отсчетов. В этом случае А = 0,95123, а выходной сигнал определяется по выражению yi = 0,95123уi-1+ 0,04877хi. С увеличением постоянной времени относительно времени между отсчетами tотс приближение к реальному НЧ-фильтру улучшается.
Для обработки данных, уже представленных в виде дискретных отсчетов, как, например, массив данных в компьютере, возможно, предпочтительней использовать такой фильтр. Рекурсивный фильтр при этом будет реализовываться с помощью однократного прохода по данным с тривиальной арифметической обработкой. Программа НЧ-фильтра на языке Фортран будет выглядеть следующим образом:
А = ехр(-TS/TC)
В = 1. — А
DO 10I = 2,N
10X(I) = А*Х(I—1) + В*Х(I),
где X- матрица данных, TS-интервал времени между отсчетами (т. е. TS = l/fOTC), а ТС-выбранная постоянная времени фильтра. Эта маленькая программа осуществляет фильтрацию на месте, т. е. она заменяет первоначальные данные отфильтрованными. Можно, конечно, создавать из отфильтрованных данных отдельный массив.
НЧ-фильтр с коммутацией. Такой же фильтр можно построить аппаратным путем, используя схему, показанную на рисунке.
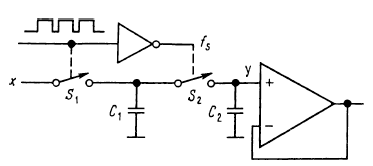
Ключи на полевых транзисторах S1 и S2 коммутируются с некоторой тактовой частотой, периодически заряжая конденсатор С1 до входного напряжения и затем передавая его заряд на конденсатор С2. Если С2 имеет напряжение U2, а С1 заряжается до входного уровня U1, то при подключении С1 к С2 напряжение на обоих конденсаторах будет определяться соотношением U = (C1U1 + C2U2)/(C1 + С2), что эквивалентно рассмотренному ранее рекурсивному фильтру при
yi=C2/(C1+C2) yi-1+C1/(C1+C2)xi
Приравнивая эти коэффициенты к заданному ранее значению А, получим
fз дБ = (1/2π)fотсln(С1 + С2)/С2.
Этот фильтр практичен во всех отношениях и обладает одной привлекательной особенностью — электронной настройкой посредством тактовой частоты fотс. В обычных схемах используются КМОП- ключи, а емкость С1 берется много больше С2. Поэтому сигнал переключения должен быть несимметричным и большую часть времени тратить на замыкание S1.
Приведенная схема представляет собой простой пример фильтра с коммутацией. В этот класс фильтров входят фильтры, выполненные на матрицах коммутируемых конденсаторов. Они имеют периодическую частотную характеристику, что делает их удобными для использования в качестве гребенчатых и узкополосных режекторных фильтров.
Для всех фильтров классического типа (Баттерворта, Чебышева и т.п.) можно построить их приближенные дискретные аналоги в форме ВЧ, НЧ, полосовых и заграждающих фильтров, как симметричных во времени, так и с истинным временем запаздывания. Такие фильтры очень удобны при обработке квантованных данных, перед которыми, безусловно, большое будущее.
Существует большое число недорогих ИМС фильтров с коммутируемыми конденсаторами. ИМС MF4 фирмы National, например, является 4- звенным НЧ-фильтром Баттерворта, размещенным в корпусе мини-DIP. Он не требует внешних компонентов и работает от одного источника питания с напряжением от 4-5 до 4-14 В. Частота среза фильтра (0,1 Гц мин. и 20 кГЦ макс.) устанавливается с помощью внешней тактовой частоты fтакт =100f3дБ. ИМС MF5 и MF10 («универсальные фильтры с коммутируемыми конденсаторами») работают несколько иначе.
С помощью внешних резисторов устанавливаются тип фильтра (ВЧ, НЧ, полосовой, заграждающий) и характеристика фильтра (Баттерворта, Чебышева и т. п.), а с помощью тактовой частоты, как и раньше, устанавливается частота среза. Другими изготовителями фильтров с коммутируемыми конденсаторами являются фирмы American Microsystems (AMI), Linear Technology (LTC) и Reticon. Фирма LTC, как всегда, использовала несколько хитроумных приемов для улучшения технических характеристик. Ее фильтры LTC1062 и МАХ280 похожи на MF4, но являются 5-звенными и имеют нулевую ошибку на постоянном токе! Последнее свойство реализовано путем размещения фильтра вне пути постоянного тока.
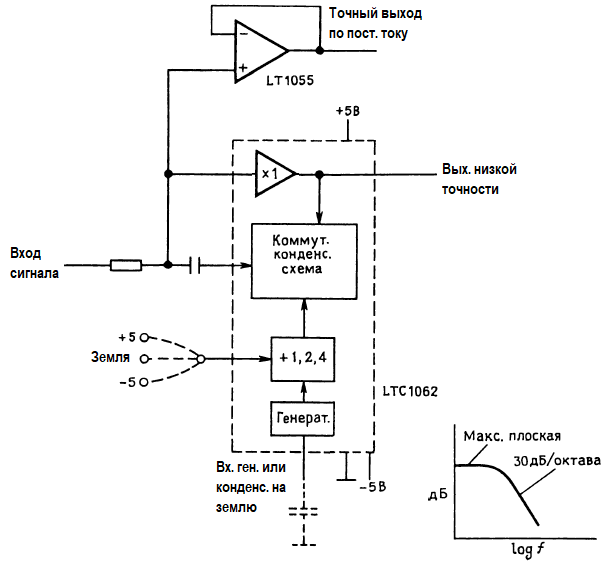
Гибкие фильтры серии МАХ260 допускают управление важными параметрами фильтра от микропроцессора.
Вообще говоря, такие фильтры с коммутируемыми конденсаторами работают только на верхнем конце звукового диапазона. В них также наблюдается существенное проникновение тактовой частоты на выход обычно в пределах 10-25 мВ. Это ограничивает их динамический диапазон в тех применениях, где тактовая частота находится внутри полосы пропускания (например, ВЧ-фильтры). Они могут иметь значительный шум, ограничивающий динамический диапазон до 80 дБ и менее (сравните со 140 дБ и выше для хорошего операционного усилителя). С другой (положительной) стороны, фильтры на коммутируемых конденсаторах просты в применении и позволяют осуществлять эффективную настройку (с помощью тактовой частоты). Фильтры такого типа широко используют в модемах (при передаче данных по телефонным линиям) и в других областях связи.
Формирование синусоидальных колебаний цифровым способом. С нерекурсивной цифровой фильтрацией связан интересный способ синтеза синусоидальных колебаний с использованием взвешенных сумм сигналов с выходов счетчика Джонсона (кольцевой счетчик с коэффициентом пересчета, вдвое превышающим число разрядов). Схема, приведённая на рисунке, показывает способ реализации такого генератора.