Конструкции активных фильтров
Известны очень хитроумные конструкции активных фильтров, каждый из которых используется для того, чтобы в качестве характеристики фильтра получить нужную функцию, как, например, функция Баттерворта, Чебышева и др. Можно спросить: зачем вообще нужно больше одной схемы активного фильтра? Причина в том, что каждая схемная реализация является наилучшей в смысле тех или иных желательных свойств, и поэтому «абсолютно лучшей» схемы активного фильтра не существует.
Некоторые свойства, желательные для схемы активного фильтра:
а) малое число элементов, как активных, так и пассивных;
б) легкость регулировки;
в) малое влияние разброса параметров элементов, в особенности значений емкостей конденсаторов;
г) отсутствие жестких требований к применяемому операционному усилителю, в особенности требований к скорости нарастания, ширине полосы пропускания и полному выходному сопротивлению;
д) возможность создания высокодобротных фильтров;
е) нечувствительность характеристик фильтра по отношению к параметрам элементов и коэффициенту усиления ОУ (в частности, произведению коэффициента усиления на ширину полосы пропускания, fс).
По многим причинам последнее свойство является одним из наиболее важных. Фильтр, который требует соблюдения высокой точности значений параметров элементов, трудно настраивать, и по мере старения элементов настройка теряется. Кроме того дополнительной неприятностью является требование использовать элементы с малым допуском значений параметров.
Схема фильтра на ИНУН (источник напряжения, управляемый напряжением) обязана широкой популярностью в основном своей простоте и малому числу деталей, но эта схема страдает недостатком, а именно высокой чувствительностью к изменениям значения параметров элементов. Интерес к более сложным гиратороподобным схемам вызван их нечувствительностью к малым изменениям параметров элементов.
Схемы на источнике напряжения, управляемом напряжением
Фильтр на источнике напряжения, управляемом напряжением (ИНУН), известный также просто как фильтр с управляемым источником, – это вариант фильтра Саллена и Ки. В этом случае повторитель с единичным коэффициентом усиления заменен неинвертирующим усилителем с коэффициентом усиления, большим 1. На рисунке даны схемы для реализации фильтра нижних и верхних частот, а также полосового фильтра.
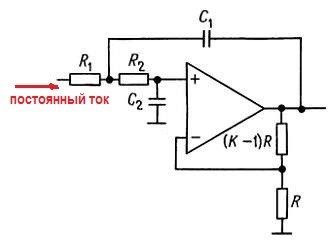
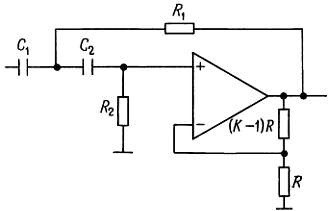
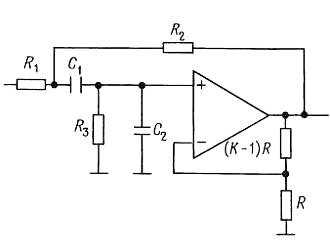
С помощью присоединенных к выходу ОУ резисторов, образован неинвертирующий усилитель напряжения с коэффициентом усиления К. Остальные R и С по прежнему формируют частотную характеристику фильтра. Как будет показано далее, эти двухполюсные фильтры могут быть фильтрами Баттерворта, Бесселя и др. за счет определенного подбора параметров элементов. Любое число двухполюсных секций на ИНУН может быть соединено каскадно для создания фильтров более высокого порядка. В таком соединении отдельные секции, вообще говоря, не идентичны. Действительно, каждая секция соответствует квадратичному сомножителю полинома степени n , описывающего фильтр в целом.
Проектирование фильтров на ИНУН с использованием упрощенных таблиц
Перед тем как пользоваться таблицей, приведенной ниже, надо решить, какая характеристика фильтра нам нужна. Фильтр Баттерворта хорош, если нужна максимально плоская характеристика в полосе пропускания. Фильтр Чебышева обеспечивает наиболее крутой спад от полосы пропускания к полосе задерживания (ценой некоторой неравномерности характеристики в полосе пропускания). Фильтр Бесселя имеет наилучшую фазочастотную характеристику, т. е. постоянное запаздывание сигнала в полосе пропускания и соответственно хорошую переходную характеристику.
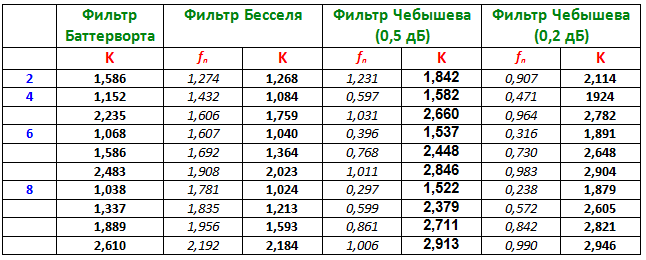
Амплитудно частотные характеристики всех этих типов даны на соответствующих графиках нормированных частотных характеристик 2‑, 4‑, 6‑ и 8‑полюсных фильтров из таблицы
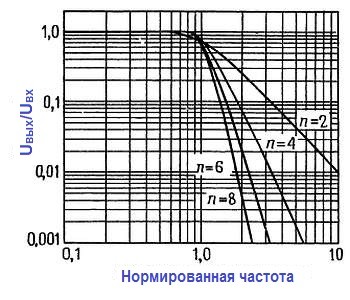

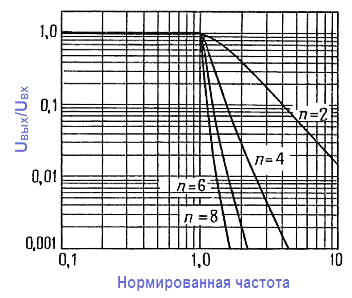
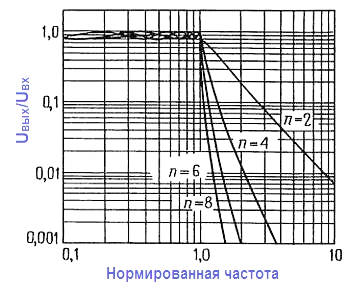
Для конструирования n‑полюсного фильтра (при четном n) нужно соединить каскадно n/2 секций на ИНУН. Рассматриваются только фильтры четного порядка, поскольку для фильтра нечетного порядка нужно столько же операционных усилителей, сколько и для фильтра на единицу большего порядка. В каждой секции R1 = R2 = R и C1 = С2 = С. Как и обычно в схемах на операционных усилителях, значение R выбирается в диапазоне от 10 до 100 кОм.
Резисторов с малым номиналом сопротивления лучше избегать, поскольку на высоких частотах возрастающее выходное полное сопротивление разомкнутого контура операционного усилителя добавляется к сопротивлению резистора, внося ошибку в расчет.
Все, что нужно сделать – это установить коэффициент усиления каждого каскада К согласно табличным данным. Для n полюсного фильтра потребуется n/2 обращений к таблице по числу секций.
Фильтры Баттерворта нижних частот
Если используется фильтр Баттерворта, то параметры всех секций имеют одинаковые значения R и С, определяемые соотношением RC = 1/2πfс, где fс – частота, соответствующая значению ослабления всего фильтра, равному – 3 дБ. Чтобы построить, например, 6‑полюсный фильтр Баттерворта нижних частот, необходимо соединить каскадно три вышеописанные секции с коэффициентами усиления, равными соответственно 1,07, 1,59 и 2,48 (желательно именно в указанном порядке, во избежание возни с динамическим диапазоном) и подбором идентичных для всех секций параметров R и С устанавливаем точку, отвечающую значению –3 дБ.
Фильтры нижних частот Бесселя и Чебышева
Ненамного сложнее построить на ИНУН фильтр Бесселя или Чебышева. Опять‑таки соединим каскадно несколько двухполюсных фильтров на ИНУН с предписанным для каждой секции коэффициентом усиления. Снова в каждой секции зададим R1 = R2 = R и C1 = С2 = С. Но теперь, в отличие от ситуации с фильтром Баттерворта, произведение RC будет для каждой секции свое и должно вычисляться с помощью нормирующего множителя fn (его значения для каждой секции приведены в таблице 1) по формуле
RC= 1/2πfсfn
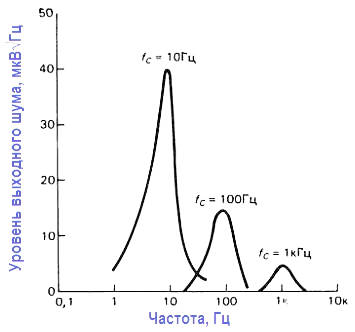
Здесь через fc обозначена точка, отвечающая значению –3 дБ, для фильтра Бесселя и граница полосы пропускания – для фильтра Чебышева, т. е. это частота, на которой амплитудно‑частотная характеристика спадает ниже диапазона неравномерности при переходе к полосе задерживания. Например, характеристика фильтра Чебышева нижних частот с неравномерностью 0,5дБ и fc=100Гц будет плоской с небольшой неравномерностью от 0 до –0,5 дБ в диапазоне от 0 до 100 Гц, на частоте 100 Гц будет затухание 0,5 дБ, а дальше частоты 100 Гц ‑ крутой спад. Значения параметров приведены в таблице 1 для фильтров Чебышева, имеющих неравномерность характеристики в полосе пропускания 0,5 и 2 дБ.
Фильтры верхних частот
Чтобы построить фильтр верхних частот, используем показанную ранее конфигурацию фильтра нижних частот, т. е. поменяем местами R и С . При этом для фильтра Баттерворта ничего больше не изменится (значения R, С и К останутся те же). Для фильтров Бесселя и Чебышева сами значения К останутся те же, а нормирующий множитель fn должен быть обратный, т. е. для каждой секции новое значение равно fn = 1/ fn (как указано в таблице 1).
Полосовой фильтр получается при каскадном соединении фильтров верхних частот и фильтров нижних частот с перекрывающимися полосами пропускания. Полосноподавляющий же фильтр можно получить с помощью схемы сложения выходных сигналов фильтров верхних частот и фильтров нижних частот с неперекрывающимися полосами пропускания. Однако такие каскадные фильтры не очень пригодны там, где нужны фильтры с высокой добротностью (полосовые фильтры с крутой переходной областью) вследствие большой чувствительности индивидуальных (непарных) фильтровых секции к значениям параметров элементов. В таких случаях следует применять высокодобротную однокаскадную полосовую схему вместо многокаскадного фильтра.
Т. е. описанную ранее полосовую схему на ИНУН или рассматриваемые далее биквадратные фильтры и фильтры на основе метода переменных состояния.
Даже однокаскадный двухполюсный фильтр может иметь характеристику с крайне острым пиком. Информацию о таких конструкциях фильтров можно найти в справочниках.
В фильтрах на ИНУН используется минимальное число элементов (один операционный усилитель на два полюса характеристики), при этом они дают дополнительный выигрыш в виде неинвертирующего коэффициента усиления, низкого выходного полного сопротивления, малого разброса значений параметров, простоты регулировки коэффициента усиления и способности работать при большом коэффициенте усиления или высокой добротности. Их недостаток – высокая чувствительность к изменениям параметров элементов и коэффициента передачи усилителя, кроме того, они не годятся для построения перестраиваемых фильтров с устойчивой характеристикой.
Фильтры, построенные на основе метода переменных состояния
Изображенный на рисунке ниже двухполюсный фильтр куда более сложен по сравнению с фильтрами на ИНУН.
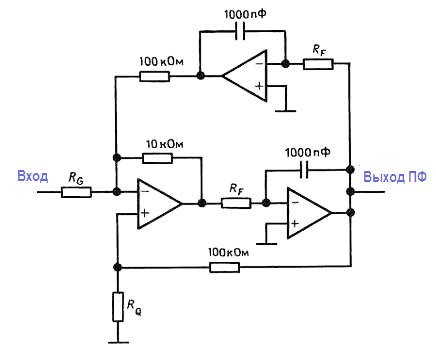
Тем не менее, он широко применяется благодаря повышенной устойчивости и легкости регулировки. Он называется фильтром на основе метода переменных состояния.
Этот фильтр выпускается в виде интегральной схемы фирмами National (AF100 и AF150), Burr‑Brown (серия UAF) и другими. Поскольку этот фильтр является готовым модулем, то все элементы у него встроенные, за исключением резисторов RG, RQ и двух RF . Среди прочих достоинств этой схемы существенна возможность путем коммутации выходов получать из одной схемы фильтры верхних и нижних частот, а также полосовой фильтр. Кроме того, частоту фильтра можно регулировать при неизменном значении добротности Q (или неизменной полосе пропускания – по выбору) характеристики в полосе пропускания. Как при работе с фильтрами на ИНУН, несколько секций могут быть соединены каскадно для создания фильтров более высоких порядков.
Изготовители этих интегральных схем предлагают для пользователей подробные расчетные формулы и таблицы. Они дают рекомендации по выбору номиналов сопротивлений внешних резисторов для получения фильтров Баттерворта, Бесселя и Чебышева разных порядков. При этом можно получать фильтры с характеристиками верхних, нижних частот или полосовые и полосноподавляющие. Привлекательной особенностью этих гибридных схем является то, что в модуль встроены конденсаторы; так что остается добавить только внешние резисторы.
Полосовые фильтры
Несмотря на большое число схемных элементов, фильтр, построенный на основе метода переменных состояния, представляется наиболее удачной схемой для реализации (высокодобротных) полосовых фильтров. Он обладает низкой поэлементной чувствительностью, не предъявляет высоких требований к ширине полосы пропускания ОУ, а также прост в настройке. Например, в представленной выше схеме, используемой в качестве полосового фильтра, с помощью двух резисторов RF устанавливается центральная частота полосы пропускания, в то время как резисторы RQ и RG совместно определяют добротность Q и коэффициент усиления в полосе пропускания
RF = 5,03·107/f0 Ом,
RQ = 105/(3,48Q + G – 1) Ом,
RG = 3,16·104Q /G Ом.
Следовательно, можно сделать настраиваемый по частоте фильтр с фиксированной добротностью Q при использовании в качестве резистора RF двухсекционного переменного резистора (потенциометра). С другой стороны, переменным можно сделать резистор RQ , при этом получается фильтр с фиксированной частотой и изменяемой добротностью Q (и, к сожалению, с переменным коэффициентом передачи).
На рисунке изображена полезная модификация полосового фильтра на основе метода переменных состояния.
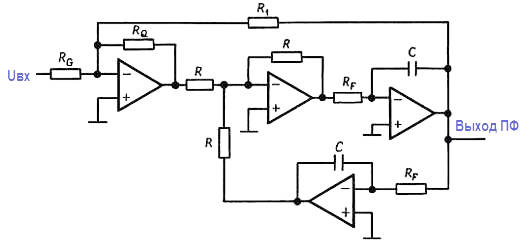
Недостатком является использование в ней четырех ОУ, достоинство же заключается в возможности регулировать ширину полосы пропускания (т. е. добротность Q) без изменения коэффициента усиления в полосе. Действительно, как добротность Q , так и коэффициент усиления устанавливаются единственным резистором. Добротность Q , коэффициент усиления и центральная частота полосы пропускания полностью независимы и задаются следующими простыми соотношениями:
f 0=1/2πRFC , Q=R1/RQ , G=R1/RG ,
R ~= 10 кОм (значение некритично, подгоняемое).
Биквадратные фильтры
Наиболее близко к фильтру на основе метода переменных состояния примыкает изображенный на рисунке так называемый биквадратный фильтр.
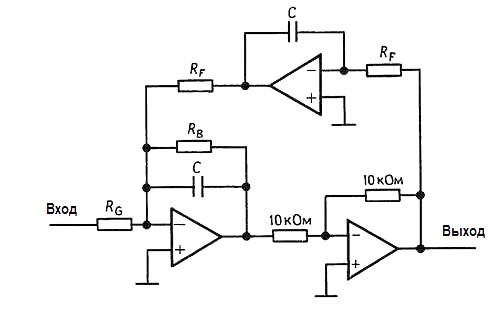
В этой схеме также используются три ОУ и ее можно сконструировать с помощью упомянутой ранее ИС на основе метода переменных состояния.
Замечательным свойством такого фильтра является возможность регулировки его частоты (с помощью RF) при сохранении постоянности ширины полосы пропускания (это предпочтительнее, чем сохранение неизменности добротности Q). Далее предлагаются расчетные уравнения:
f 0 = 1/2πRFC, BW = 1/2πRBC, G = RB /RG .
Сама добротность Q определяется как f0/BW и равна RB /RF . При изменении значения центральной частоты (с помощью RF) пропорционально изменяется и добротность Q , при этом сохраняется неизменной ширина полосы пропускания Qf0 .
Когда проектируется биквадратный фильтр вчерновую (правильнее использовать ИС активного фильтра, которая уже содержит большинство необходимых элементов), то основная методика определяется следующим образом:
- Выберем ОУ с шириной полосы пропускания fс, которая, по крайней мере, в 10–20 раз превышает Qf0.
- Подберем округленный номинал конденсатора, ближайший к следующему значению С = 10/f0 мкФ.
- Используем требуемое значение центральной частоты для расчета значения сопротивления RF согласно приведенному выше первому уравнению.
- Используем второе расчетное уравнение для вычисления по заданному значению ширины полосы пропускания номинала сопротивления RG.
- Исходя из требуемого коэффициента передачи на центральной частоте полосы пропускания и, согласно третьему расчетному уравнению, получаем значение сопротивления RG.
Если расчетные значения сопротивлений получаются слишком велики или слишком малы, что неудобно в некоторых случаях, то можно подобрать другой номинал конденсатора. Например, в высокодобротном фильтре потребуется использовать увеличенное значение конденсатора С, отчасти с тем, чтобы предотвратить существенное увеличение значение сопротивления RB. Следует отметить, что каждое из сопротивлений RF, RB и RG является нагрузкой для ОУ и, следовательно, их значение не должно становиться меньше, скажем, 5 кОм.
Манипулируя номиналами элементов схемы, можно найти их значения, так чтобы просто удовлетворялось требование 1. Это достигается путем уменьшения коэффициента передачи интегратора (увеличение значения RF) при соответствующем увеличении коэффициента передачи инвертирующего каскада (увеличение значения резистора обратной связи, которое в исходной схеме составляет 10 кОм).
Полосовые фильтры высокого порядка
Как и для рассмотренных ранее фильтров нижних и верхних частот имеется возможность проектировать полосовые фильтры более высоких порядков с приблизительно плоской полосой пропускания и крутым переходом к полосе задерживания. Это можно сделать с помощью каскадного соединения нескольких полосовых фильтров более низкого порядка. Их необходимо комбинировать таким образом, чтобы обеспечить характеристику фильтра требуемого вида (Баттерворта, Чебышева и любые другие). Как и раньше фильтр Баттерворта имеет «максимально плоскую» характеристику. В то время как фильтр Чебышева удовлетворяет требованиям плоской характеристики в полосе пропускания при крутых скатах (переходной области).
Только что рассмотренные полосовые схемы, такие как фильтры на ИНУН, биквадратные фильтры и фильтры на основе метода переменных состояния, являются фильтрами второго порядка (два полюса). Увеличение крутизны характеристики фильтра путем добавления дополнительных секций приводит, как правило, к ухудшению переходной и фазо‑частотной характеристик. Сама «ширина полосы пропускания» полосового фильтра определяется как ширина характеристики между точками –3 дБ. Кроме, естественно, равноволновых фильтров, для которых эта ширина определяется точками, где характеристика спадает на величину пульсации в полосе пропускания.
В справочниках по активным фильтрам или в технических руководствах по применению ИС активных фильтров приводятся таблицы и методики проектирования таких сложных фильтров.
Двойной Т-образный фильтр-пробка
Изображенная на рисунке пассивная RC‑цепь имеет бесконечное затухание на частоте, равной fc = 1/2πRC.
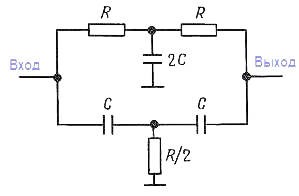
Такое бесконечное ослабление для RС‑фильтров, вообще говоря, не характерно – данный фильтр действует столь эффективно благодаря сложению двух сигналов, которые на частоте среза имеют разность фаз в 180°. Получение достаточно близкого к нулю значения характеристики на частоте fc требует хорошего согласования элементов. Этот фильтр называется двойным Т‑образным и может употребляться для устранения сигнала помехи, например сетевой наводки 50Гц.
Трудность состоит в том, что характеристика этой цепи такая же «мягкая», как и у всех пассивных RC‑цепей, и лишь в окрестности частоты fc обрывается почти отвесно. Например, двойная Т‑образная цепь, управляемая идеальным источником напряжения, имеет затухание 10 дБ на частоте, равной удвоенной (или половинной) частоте fc. Также имеет ослабление 3 дБ на частоте, равной учетверенной (или деленной на четыре) частоте fc. Один из способов улучшить характеристику этой цепи – сделать ее «активной». По типу фильтра Саллена и Ки.
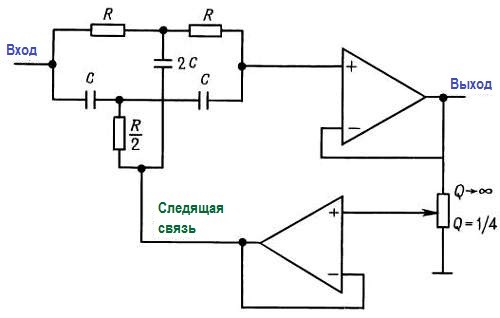
Эта идея кажется в принципе хорошей, но на практике разочаровывает из‑за невозможности сохранения хорошего затухания на частоте нуля. Дело в том, что при увеличении резкости провала характеристики (большее усиление в петле следящей связи) ослабление на частоте нуля уменьшается.
Двойные Т‑образные фильтры выпускаются в виде готовых модулей на диапазон частот от 1 Гц до 50 кГц с глубиной ослабления на частоте провала около 60 дБ (с некоторым ухудшением при высоких и низких температурах). Такие фильтры легко собрать из отдельных элементов, но для получения глубокого и стабильного провала следует выбирать конденсаторы и резисторы со стабильными параметрами и низкой температурной зависимостью. Один из элементов должен быть регулируемым.
Двойной Т‑образный фильтр функционирует прекрасно при фиксированной частоте провала, но основные трудности возникают при попытке сделать его перестраиваемым, поскольку три резистора необходимо изменять одновременно, сохраняя постоянным их соотношение. Однако замечательная своей простотой, изображенная на рисунке RC‑схема, которая ведет себя аналогично двойной Т‑образной схеме, может перестраиваться в широком диапазоне частот (по крайней мере, две октавы) с помощью единственного потенциометра.
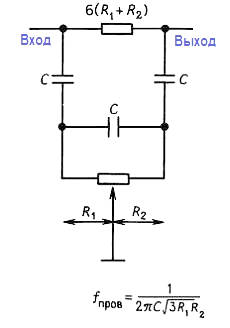
Подобно двойному Т‑образному фильтру (как и большинство активных фильтров), для него требуется провести определенное согласование элементов. В этом случае номиналы всех трех конденсаторов должны быть идентичны, а значение фиксированного резистора должно точно в шесть раз превышать значение нижнего (регулируемого) резистора. Сама частота подавления определяется следующим образом:
fпровала = 1/2пС √ (3R1R2)
На следующем рисунке показана реализация этого фильтра, которая перестраивается в диапазоне от 25 до 100 Гц. Подстроечный резистор с номиналом 50 кОм позволяет установить максимальную глубину провала.
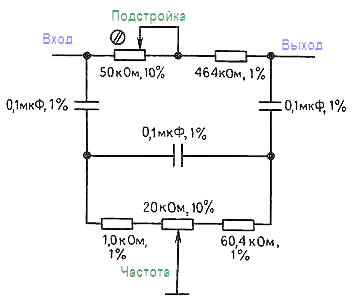
Как и в случае пассивной двойной Т‑образной схемы, этот фильтр (известный как мостовой дифференциатор) имеет пологое нарастание затухания за пределами точки провала и бесконечное затухание (при условии идеального согласования значений всех элементов) на самой частоте провала. Его также можно «активировать» с помощью подачи на отвод потенциометра следящей связи с усилителя напряжения, как правило, с коэффициентом передачи меньше единицы.
Увеличение коэффициента передачи в петле следящей связи, а именно его приближение к единице, сужает ширину провала, а также приводит к появлению нежелательного пика характеристики со стороны более высоких частот относительно провала, наряду со снижением обеспечиваемого затухания.
Построение фильтров на гираторах
Интересный тип активного фильтра можно создать с помощью гираторов. В основном они используются для замены катушек индуктивности в традиционных конструкциях фильтров. Распространенная гираторная схема показана на рисунке.
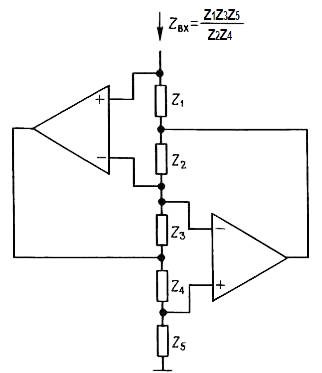
Обычно Ζ4 – конденсатор, а остальные полные сопротивления заменяют резисторами. Таким образом имитируется катушка индуктивности L = kС, где
k = R1R3R5/R2.
Можно показать, что эта гираторная схема мало чувствительна к отклонениям параметров, как и ее пассивный RLC‑прототип.
Фильтры на переключаемых конденсаторах
Один из недостатков биквадратных фильтров или фильтров, построенных на основе метода переменных состояния, связан с необходимостью обеспечения точного согласования конденсаторов. Если при построении схемы используются операционные усилители, то вам следует запастись парой стабильных конденсаторов (не керамических и не электролитических). Для обеспечения оптимальных рабочих характеристик точность их согласования порядка 2 %.
Необходимо также провести многочисленные коммутации, поскольку эти схемы содержат, по крайней мере, три ОУ и шесть резисторов на каждую двухполюсную секцию фильтра. С другой же стороны, можно купить фильтр в виде ИС, предоставляя право изготовителям самим решать проблему согласования конденсаторов с номиналом 1000 пФ в своей ИС. И, надо сказать, что изготовители ИС успешно решают эти проблемы, но за счет увеличения их стоимости. Например, ИС AF100‑«универсальный активный фильтр» производства фирмы National представляет собой гибридную ИС.
Известен и другой способ построения интеграторов, которые составляют основу биквадратных фильтров и фильтров на основе метода переменных состояния. Главная идея заключается в использовании аналоговых МОП‑ключей. МОП‑ключи синхронизированны внешним сигналом прямоугольной формы и высокой частоты (как правило, в 100 раз выше, чем у обрабатываемых аналоговых сигналов), как это показано на рисунке.


На этом рисунке необычный треугольный объект представляет собой цифровой инвертор, который переворачивает прямоугольное колебание «вверх ногами», так что два МОП‑ключа замыкаются на противоположных полуволнах этого прямоугольного колебания. Анализ такой схемы весьма прост. При замыкании ключа S1 происходит заряд конденсатора С1 до напряжения Uвх, т. е. он сохраняет заряд С1Uвх. На другой же половине рабочего цикла конденсатор С1 разряжается через виртуальную землю, передавая свой заряд конденсатору С2. Само же напряжение на конденсаторе С2 изменяется, следовательно, на величину ΔU = ΔQ /C2 = UвхC1 /C2.
Следует отметить, что выходное напряжение меняется в течение каждого цикла высокочастотного прямоугольного колебания пропорционально напряжению Uвх (изменение которого за один период прямоугольного колебания предполагается весьма незначительным), т. е. эта схема представляет собой интегратор! Легко показать, что функционирование этих интеграторов описывается приведенными на рисунках уравнениями.
Применение переключаемых конденсаторов вместо обычных интеграторов дает два существенных преимущества. Первое, как было указано ранее, он может быть менее дорогим при реализации на кремниевой подложке, так как коэффициент передачи самого интегратора зависит только от отношения двух конденсаторов, а не их индивидуальных значений.
Вообще говоря, достаточно просто на кремниевой подложке создать пару любых согласованных элементов, в то время как получение подобных элементов (резистора или конденсатора) с точными значениями и высокой стабильностью весьма затруднительно. Вследствие, этого монолитная ИС фильтра на переключаемых конденсаторах очень дешевая.
Второе преимущество фильтров на переключаемых конденсаторах состоит в возможности настройки их частоты (т. е. центральной частоты полосового фильтра или точки – 3 дБ фильтра нижних частот) изменением только частоты входного прямоугольного колебания («тактовой частоты»). Это объясняется тем, что характеристическая частота биквадратного фильтра или фильтра на основе переменных состояния пропорциональна и зависит только от коэффициента передачи интегратора.
Фильтры на переключаемых конденсаторах выпускаются как в виде специализированной, так и «универсальной» структуры. Первая структура со встроенными компонентами формирует полосовые фильтры или фильтры нижних частот, в то время как вторая имеет дополнительные промежуточные входы и выходы, так что при подключении к ней внешних элементов можно получить любую желаемую характеристику. При этом платой за такую универсальность является увеличение размера корпуса ИС и необходимость в подключении внешних резисторов.
Например, автономный фильтр Баттерворта нижних частот MF4 фирмы National выпускается в 8‑выводном DIP‑корпусе, в то время как их универсальный фильтр MF5 выпускается в 14‑выводном DIP‑корпусе. При этом в зависимости от выбора типа фильтра требуется 2 или 3 внешних резистора. На рисунке показано с какой легкостью можно использовать эти специализированные фильтры.
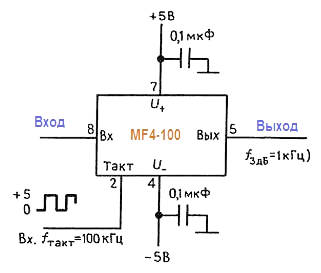
Теперь о неприятном. Фильтры на переключаемых конденсаторах имеют три «раздражающие» характеристики, которые связаны и обусловлены присутствием периодического тактового сигнала. Первое, это сквозное прохождение сигнала тактовой частоты, а именно наличие некоторого выходного сигнала (с напряжением приблизительно от 10 до 25 мВ) с частотой тактового колебания, напряжение которого не зависит от прикладываемого входного сигнала.
Обычно это не имеет значения, поскольку этот сигнал значительно удален от полосы, занимаемой обрабатываемым сигналом. Если же такое сквозное прохождение тактового сигнала нежелательно, то для его подавления обычно используется простой RC‑фильтр. Вторая проблема более тонкого свойства. Если во входном сигнале присутствуют спектральные компоненты, расположенные вблизи частоты тактового колебания, то они будут «накладываться» на полосу пропускания. Сформулируем это более корректно, а именно:
любые спектральные компоненты входного сигнала, которые отстоят по частоте от тактового сигнала на величину, соответствующую частотам полосы пропускания, будут присутствовать (неподавленными!) в полосе пропускания.
Например, при использовании ИС MF4 в качестве фильтра нижних частот с частотой среза 1 кГц (т. е. при этом fтакт = 100 кГц) все спектральные компоненты входного сигнала в диапазоне от 99 до 101 кГц выделятся в полосе выходного сигнала, т. е. в диапазоне от постоянного тока до частоты 1 кГц. И никакой дополнительный выходной фильтр не сможет их ликвидировать!
Таким образом, следует твердо уяснить, что во входном сигнале не должно быть спектральных составляющих вблизи частоты тактового колебания. Если же этого невозможно избежать, то можно как обычно использовать простой RС‑фильтр (предфильтр), поскольку частота тактового сигнала отстоит, как правило, довольно далеко от полосы пропускания.
Третье нежелательное свойство, присущее фильтрам на переключаемых конденсаторах, связано с типичным снижением динамического диапазона сигнала (возрастание уровня «шума»), вследствие неполного гашения инжекции заряда МОП ключа. В типовой ИС фильтра динамический диапазон составляет 80–90 дБ.
Как и для любой линейной схемы, фильтрам на переключаемых конденсаторах (и их аналогам на трех ОУ) присущи характерные ошибки усилительных схем. А именно выходное напряжение смещения и низкочастотный шум с характеристикой вида 1/f . Это может стать проблемой, если, например, нежелательно при подаче на фильтр нижних частот сигнала низкого уровня получать ошибки в виде колебания среднего значения его постоянной составляющей. Прекрасное решение предложили умные головы фирмы Linear Technology, которые придумали ИС LTC1062 – «фильтр нижних частот с точным значением постоянной составляющей» (или МАХ280 с улучшенным напряжением смещения). На рисунке показан способ ее включения.
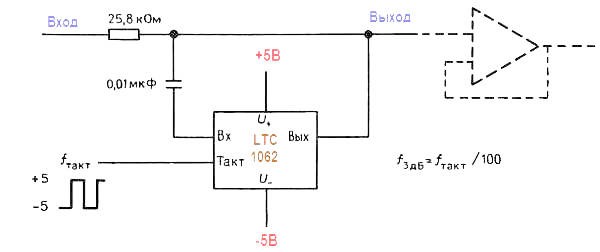
Основная идея состоит в том, чтобы вывести фильтр из пути прохождения постоянной составляющей, пропуская низкочастотные компоненты сигнала на выход через пассивную цепь. Сам же фильтр захватывает только более высокочастотные компоненты сигнала, где он заваливает характеристику, шунтируя сигнал на землю. В результате этого ошибка в постоянной составляющей равна нулю, а характерный для переключаемых конденсаторов шум присутствует только в непосредственной близости от частоты среза.